|
|
Backgammon AI |
Computer Backgammon
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Originally published in Scientific American, vol. 242, no. 6 (June 1980), pp. 64–72. |
 |
The photograph on the cover shows a computer-graphics display of a critical position in the fifth and final game of a backgammon match between the world backgammon champion, Luigi Villa, and a computer program, BKG 9.8. The program, which defeated Villa by the score of 7–1, became the first computer program to beat a world champion at any board or card game. Villa had the white pieces and moved clockwise; BKG 9.8 had the orange pieces and moved counterclockwise. In this position BKG 9.8, which had rolled a five and a one on the dice, made a sensational play that surprised its programmers and won the applause of the experts who watched the game. The computer-graphics display was provided by the Three Rivers Computer Corporation of Pittsburgh. |
| Backgammon is a good test of principles of artificial intelligence. BKG 9.8 is the first computer program to defeat a world champion at any board or card game. |
Last July my backgammon-playing computer program BKG 9.8 defeated the world champion, Luigi Villa of Italy, by the score of 7–1 in a $5,000 winner-take-all match in Monte Carlo. It was the first time a computer program had beaten a world champion at any board or card game. Before the match Paul Magriel, the former world backgammon champion who had provided some of the expert knowledge that went into the development of BKG 9.8, estimated that the program had between a 35 and a 40 percent chance of winning. I had thought he was overly enthusiastic. The program did get the better of the dice rolls, but it also played with great accuracy and imagination and clearly emerged the victor. Unlike the best programs for playing chess, BKG 9.8 does well more by positional judgment than by brute calculation. This means that it plays backgammon much as human experts do.
My work on computer backgammon is part of the large branch of computer science called artificial intelligence, which aims at developing programs capable of doing things that if a human being were to do them, he would be considered intelligent. Investigators in artificial intelligence have always been interested in games because intelligence is needed to play them well. The rules of a game are precisely defined and there are usually standards of performance, so that it is often possible to pit a program directly against human competitors under controlled conditions. In this way the capacity (and hence the intelligence) of the program can be accurately measured.
For six years I worked on a chess program that I hoped would approach the game the way a human chess master does. I was reasonably well qualified to do so. For some 15 years I was one of the top 12 players in the U.S., and in 1968 I won the world correspondence-chess championship. One kind of chess program is the searching program, which is designed to investigate all possibilities to a certain depth. In the course of my work on computer chess I encountered several kinds of methodological problems with which searching programs had great difficulty. One problem is called the horizon effect, which arises when a program searches deeply enough to discover a difficulty in the play but then acts as if the difficulty did not exist. Actually the program recognizes the difficulty, but it postpones it by finding another line of play interspersing perhaps two insignificant but forced moves in that branch of the search. Since all branches are investigated to the same depth, the search is terminated before the problem is discovered in that particular branch. As a result the program acts as though it has permanently avoided the difficulty. If it had pushed a little deeper into the branch, it would have encountered the same problem.
The fact that human experts would never make this kind of mistake indicates they have a different way of approaching the game. They organize the moves into events. As long as an important event remained unexplored in any branch the expert would not terminate his search. By looking not at events but at moves the programs misplayed certain straightforward positions.

|
| King-and-pawn end game is typical of the kind of position computer programs that play chess could not cope with. This position is an example of what is called the horizon effect: the program believes it has solved a problem that in fact it has only succeeded in postponing. The program, which was playing White, was designed to choose a move in the position after investigating all possibilities to a depth of three plies (two moves for White and one move for Black). The program finds the line of play 1 P-R8(Q) P-B8(Q), 2 Q-N7 ch. (say) and correctly judges that it is ahead by two pawns and winning. It also finds, however, that by playing 1 P-Q6 ch. KxP, 2 P-R8(Q) it comes out a queen ahead, and so the program clearly prefers this continuation to the preceding one. The fact that on the next move Black will also make a queen escapes the program’s notice, since it has been told to search only to a depth of three plies. On the program’s next turn it will realize that the intended P-R8(Q) will not put it a queen ahead because of P-B8(Q), and so it again invokes and artificial remedy: 1 P-K5 ch. KxP, 2 P-R8 ch. This scenario seems absurd to human players because they approach the game in a different way. They look not at moves but at events. The queening of the black pawn is an important event, which the program noticed. As long as an important event has not been explored in a branch of the tree, a human expert would continue to study the position before making a move. |
Building positional judgment into a program was also extremely difficult. Chess masters can agree that a certain attack is worth, say, two pawns. An enormous amount of information goes into such judgments, and it is remarkable that quantitative values can be put on them. Many people would doubt that any program could possibly do such a thing. It seemed to me that introducing rules to enable a program to make such judgments would involve an incredibly large (perhaps impossibly large) number of rules to specify under what conditions a certain feature of a position is good and just how good it is. As a result I decided to examine how variables corresponding to significant features of a position could be combined into arithmetical functions to create fine shades of difference in output. Chess was not suited to such an investigation because too much of the judgment process involves playing out alternatives to see which features come to fruition in a particular position. What I wanted was a domain where it is possible to compare two situations and make a judgment about which one is the better without having to worry about the exhaustive analysis that chess positions require. When I became acquainted with backgammon, I realized it had the desired properties, and I set out to develop a backgammon program.
Let me briefly describe the rules of backgammon for those readers who are not familiar with the game. Backgammon is a dice game in which a player tries to move all 15 of his pieces out of his end of the board before his opponent does. The board consists of 24 “points,” or triangles, divided into four quadrants: inner and outer “tables” for each player. The initial position of the pieces is shown in the illustration below. The pieces are moved from point to point according to the numbers a player rolls on a pair of dice.

|
| Starting position of a backgammon game shows the pieces arranged symmetrically. The board consists of 24 red and black points that are divided into four quadrants: Black’s inner “table” (consisting of the points numbered 1 through 6), Black’s outer table (the points 7 through 12), White’s outer table (the points 13 through 18) and White’s inner table (the points 19 through 24). The pieces are moved from point to point according to the numbers rolled on dice. The white pieces move clockwise so that they follow the points in ascending order; the black pieces move counterclockwise so that they follow the points in descending order. The notation used to represent backgammon moves is easy to understand. For example, 7/10 means a piece is moved from the 7 point to the 10 point. The cube on the bar that separates the inner tables from the outer ones is called the doubling cube. The 1 indicates that the game is being played for the original stake. On any turn before a player throws the dice he can offer to double the stake by turning the cube to the face marked 2. The other player must accept or reject the offer. If he accepts, the game is played out for twice the original stake. If he declines, the game is over and he pays the original stake. Once a player accepts a double only he can offer the next one, which would quadruple the original stake. |
If the numbers on the dice are not the same, the player either uses each number to move one piece or uses the total of the two numbers to move one piece. Each number is considered individually, so that when the player uses both numbers to move one piece, he makes not one move but two separate moves. For example, if one die shows a six and the other a two, a single piece may first be moved six points and then two points (or first two points and then six points). When a piece is moved to a point for the first move of a two-move play, it is said to touch down on that point.
If the numbers rolled on the dice are the same, the player uses that number four times. For example, if he rolls two twos, he can either (1) move one piece a total of eight points, (2) two pieces four points each, (3) two pieces two points each and one piece four points, (4) one piece six points and one piece two points or (5) four pieces two points each.
When at least two pieces of one side occupy a point, the point is said to be made, and none of the opponent’s pieces can touch down or land there. A made point is quite useful because it not only blocks your opponent’s progress but also serves as a base for your own pieces. When a point has only one piece on it (called a blot), it is “hit” (sent off the board) when an opposing piece touches down or lands there. The hit blot, which is put on the bar that divides the inner and outer tables, must be reentered at the beginning of the board before the player can move another piece.
Once a player has moved all 15 pieces onto his inner table, he can begin bearing them off the board according to the numbers on the dice. The winner is the first player to bear off all his pieces. There are three kinds of victory: a normal one for an agreed stake if the loser has borne off at least one of his pieces, a gammon for twice the stake if the loser has not borne off any of his pieces and a backgammon for three times the stake if the loser has not borne off a piece and has at least one piece in his opponent’s inner table or on the bar.

|
| Color video display shows a critical position in the first game of the $5,000 winner-take-all backgammon match between the author’s computer program BKG 9.8 and the world champion, Luigi Villa of Italy. The program had the orange pieces and moved counterclockwise; Villa had the white pieces and moved clockwise. To win the game a player must first move all his pieces onto the six “points,” or triangles, in his home quadrant of the board and then move them off the board before his opponent does. The program’s home quadrant is at the top left; Villa’s home quadrant is at the bottom left. The program is ahead in the position shown because the world champion still had to move the three white pieces at the top left 16 points before they could be in his home quadrant. The position is analyzed in more detail later in the article. The color video display was provided by the Three Rivers Computer Corporation of Pittsburgh. |
What makes backgammon an exciting gambling game is an additional device called the doubling cube. On any turn before a player throws the dice he can propose a doubling of the stake by turning the doubling cube to the face marked 2. His opponent can either decline the double, in which case he concedes the game and gives up the stake or accept the double, in which case the game is played out for twice the stake. The player who accepts a double gets possession of the doubling cube, which means that he is the only one who can next propose a doubling of the current stake. The number of redoubles in games between good players is usually small, the value of the cube seldom going above 4.
Such is the nature of the game I set out to program. The basic element of any game-playing program is a move generator that takes an input position and generates all the legal moves (and only the legal moves) that can be made beyond a given position. The possible continuations are arranged in the form of a tree diagram. One branch of the tree is followed until the program encounters a reason for terminating the search. The program then applies an evaluation function to the terminal position to arrive at a quantitative value that expresses which player is in a better position and by how much. The program selects its move by comparing this value with the values it has assigned to other branches.
In chess programs the branches are usually followed to a prearranged maximum depth. The branching factor for chess (the average number of moves that can be made beyond each node in the tree diagram) is about 35, and it is possible for a fast program to search to a depth of six plies in the three minutes per move that is allotted in tournament play. In backgammon, however, the branching factor is more than 400: there are 21 possible rolls on each move and some 20 ways of playing each roll. Such a large branching factor indicates that an exhaustive search would not be the right way to design a backgammon-playing computer program.
What my program does is to generate all the legal moves in the game position and evaluate them without searching. The program selects the move with the highest evaluation and makes it in the game. The evaluation function considers such factors as the safety of the pieces, the extent to which the pieces are blockaded, the degree to which either side is ahead in the race to bear pieces off and so on. The doubling cube is also controlled by the evaluation function, which decides whether a double should be offered and whether an offer made by the opponent should be accepted or declined.
To construct an effective evaluation function calls for testing various approaches in actual programs. The evaluation function in my first program was based on a linear polynomial in which each term represented a particular feature of a backgammon position and the constant coefficient of the term indicating the importance of that feature. The sum of the linear polynomial gave the value of the position. This approach was limited by the fact that the constant coefficient could represent only the average importance of the feature. It was a limitation that frequently prevented the backgammon program from making expert judgments.
My next effort was to divide the backgammon positions into classes, each of which had a somewhat different evaluation function. This approach led to an improvement in the program’s playing strength, but it too had a drawback. The relative values of two positions in different classes were sometimes inaccurate because the evaluation functions yielded significantly different values for positions near the common border of the classes where the values should have been quite close.
For example, suppose the program has to choose between a move leading to a blockading game (in which the relevant considerations are making points, leaving blots and hitting blots) and a move leading to a running game (in which the opposing armies of pieces have passed each other, so that the only consideration is which army is ahead in the race). Moreover, in the blockading game each side must evaluate the potential running game that would come about if the armies were to suddenly disengage. Since the running game is completely different from the blockading game, the program has difficulty comparing the two. The roughness of boundaries between the two kinds of game, which occasionally led to serious errors in judgment, seemed almost impossible to remedy.
The next attempt at an evaluation function proved to be much more successful. To overcome the problem of the rough boundaries the positions were not divided into classes. Instead the evaluation space of all the positions was warped in such a way that in certain parts of the space a particular feature could be more important than it was in other parts. The transition in importance from one part of the space to another part was made to be smooth. Moreover, the transition depends on the other features present. This means that the importance of a particular feature is a nonlinear function. The features that control the transitions are called application coefficients; they are special slowly changing variables that replace the normally constant coefficients in the linear polynomial evaluation function. Since the application coefficients vary slowly and smoothly, they can provide a great deal of context but avoid the rough boundaries between different contexts. We called this new approach SNAC, for smoothness, nonlinearity and application coefficients.
The SNAC approach enabled the BKG program (the BKG stands for backgammon) for the first time to make accurate use of the vast amount of knowledge that was by now built into it. The earlier versions of the program had been limited in their ability to apply this knowledge. Each SNAC function is in effect a microstrategy for accumulating or avoiding certain features of a backgammon position. The coefficient indicates the applicability of the strategy. As a result BKG can simultaneously investigate any number of the 30 or so strategies for which it has SNAC functions, keeping track of exactly how important each strategy is in the particular position. At any point in the game some strategies may be ignored completely, other raised to the highest level of significance and still others given only moderate consideration. The approach allows a gradual shifting of strategic priorities without a sudden aberration of performance as new demands arise.
The structure and content of the program were evaluated under controlled conditions in three ways: by giving it problems from standard instructional texts, by pitting it against other programs and by having it play against human competitors. The record of the BKG program both in solving backgammon problems from texts and in playing actual backgammon games showed a marked improvement after the introduction of SNAC, in spite of the fact that the program had gained little additional knowledge of the game. In competition BKG was trouncing the best available commercial backgammon-playing microprocessor 78 percent of the time. Without SNAC, BKG had beaten the microprocessor only 56 percent of the time. When Magriel played against the program for the first time, he was surprised at how well it did. He subsequently helped us to refine the algorithms bearing on the doubling cube and to evaluate the program’s overall performance.
| |||||||||||||||
| Table of performance results shows that the program did much better when the polynomial evaluation function it used to judge the strength of a backgammon position had smooth nonlinear functions and the application coefficients (designated SNAC). In the polynomial each term represents a feature of a backgammon position, and the nonlinear coefficient of the term shows the importance of the feature. The fact that the coefficient is not constant but varying means the importance of a feature changes according to other features in the position. |
The real test of BKG’s strength came in May, 1979, when BKG 9.7 (the numbers stand for successive versions of the program) played in a small private tournament of intermediate-level players in California and won its first two matches before losing to the ultimate winner of the tournament. Without SNAC, BKG had not done well in tournaments. In the spring of 1978 the program had been eliminated from an intramural competition at Carnegie-Mellon University after it had lost its first two matches to weak players.
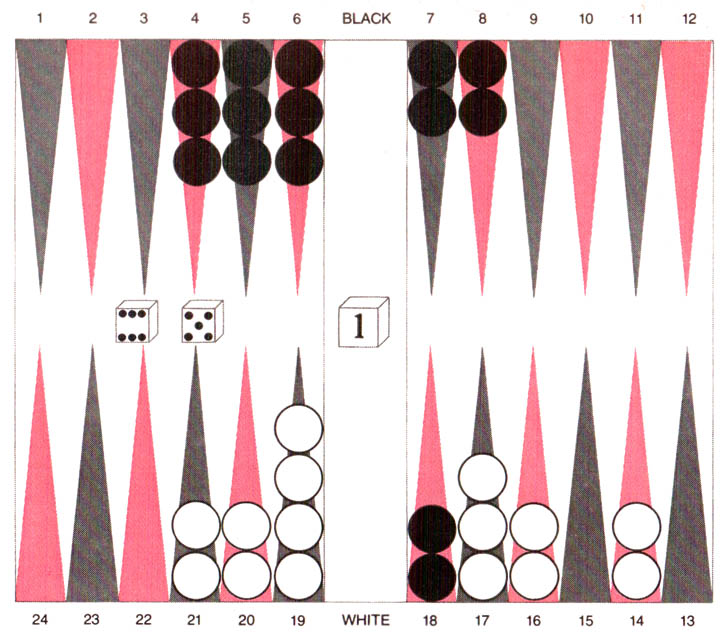
|
| This backgammon position is typical of the kind of position an early version of the BKG program could not handle well. Black has rolled a six and a five that can be played in two fundamentally different ways: running both pieces from the 18 point (18/12 and 18/13) or moving two other pieces. The first way (leading to a running game) disengages the armies of pieces, so that the rest of the game becomes a straightforward race. The second way (leading to a blockading game) leaves the armies entangled, so that considerations such as making points, leaving “blots” and hitting them are quite important. The program could have adequately compared two running-game alternatives or two blockading-game ones. Yet since the running game and the blockading are different, the program had trouble deciding which formation is better. |
The fateful week in Monte Carlo when the program would be pitted against the world champion was only a month later. Before the contestants could meet, the best human competitors had to play among themselves for the world title, which Villa eventually won.
The BKG 9.8 program, running on a PDP-10 computer at Carnegie-Mellon, was connected by satellite to a mobile robot in Monte Carlo. Not much was expected of the programmed robot, dubbed Gammonoid by the tournament organizers. Although the organizers had made Gammonoid the symbol of the tournament by putting a picture of it on their literature and little robot figures on the trophies, the players knew that existing microprocessors could not give them a good game. Why should the robot be any different?
This view was reinforced at the opening ceremonies in the Summer Sports Palace in Monaco. At one point the overhead lights dimmed, the orchestra began playing the theme of the film Star Wars and a spotlight focused on an opening in the stage curtain through which Gammonoid was supposed to propel itself onto the stage. To my dismay the robot got entangled in the curtain and its appearance was delayed for five minutes.
The match between BKG 9.8 and the champion took place at 11:00 p.m. on the last day of the tournament. Each side put up $2,500 so that the contest would be a meaningful one. To convince the spectators that the program’s dice rolls were honest the tournament director appointed an assistant to roll for the robot. The match, which was held in the Winter Sports Palace, was being carried by closed-circuit television to a room with seating for 200. Magriel was ready to provide a play-by-play commentary, but even with this added attraction the attendance was disappointingly low.
In the first game BKG 9.8 got off to a good start. It doubled appropriately at an early point, when Villa had to accept, and it skillfully nursed its advantage to get into a position where it had almost won. The illustration below shows is a key position near the end of the game. The program rolled a four and a two and was forced to leave a blot. Which blot would it leave? It could move a piece from the 5 point to the 1 point and a piece from the 4 point to the 2 point, leaving a blot on the 5 point that could be hit in 11 ways (by any dice roll with a two in it). It chose to move two pieces from the 9 point to the 5 and 7 points, leaving a blot on the 7 point that could be hit in 13 ways (by any roll of four or a roll of a three and a one).
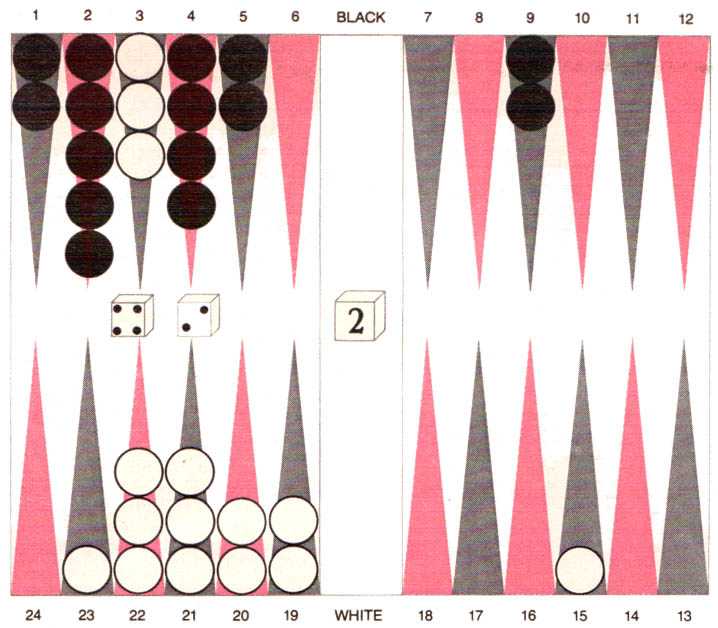
|
| BKG rolled a four and a two in this position from the first game of its match with Villa. The program (Black) had the advantage but was forced to leave a blot. It played 9/5 and 9/7, leaving a blot on the 7 point that could be hit by 13 dice rolls. The apparently safer play of 5/1, 4/2, leaving a blot on the 5 point that could be hit only by 11 rolls, is inferior because it leaves two pieces on the 9 point that could become exposed later when they must move. |
The BKG program has a function that counts the number of ways a blot can be hit, and so it completely understands the present risk of getting hit. It also has SNAC functions that measure the future risk of getting hit as a function of various kinds of formations immediately breaking up. The two plays between which the program chose differ in the balance between present risk and future risk, but the SNAC functions are well tuned for this kind of situation, and so the program has no trouble deciding which play is better. It understands that it has chosen the move with the greater present risk. Yet it also recognizes that if it had made the safer play, it would soon have had to move the pieces on the 9 point. Then it would probably have been forced to leave a blot, because the nearest friendly point is far from the 9 point. Therefore the program prefers to take a slightly greater risk immediately and do away with the long-term problem altogether. This play is certainly the correct one, which any expert should make without thinking, but it is not the kind of thing computer programs are supposed to be able to do, taking an apparently ill-advised action because it is well advised in the long run. After BKG had made the move Villa was unable to hit the blot, and BKG went on to win smoothly, making the score 2–0.
The second game was a pivotal one in the match. Again the program got off to a good start, and to keep his chances alive Villa hit one of BKG’s pieces in his own inner board. This brought about the position shown in the illustration below, with the program having the next move. Here BKG made an extremely imaginative double that Villa declined. The program realized that it already had a slightly better position and that if its next roll was good (any roll with a one, particularly a roll that enables the piece on the 4 point to be hit), it could easily swing the game very much in its favor. In that case it would be too late to double because Villa would decline, thereby depriving BKG of the possibility of gammoning him. The experts applauded the double, although they also thought Villa should have accepted it. He declined because he was hoping things would go his way in the subsequent games. The score was now 3–0, and more spectators began to come into the television room.
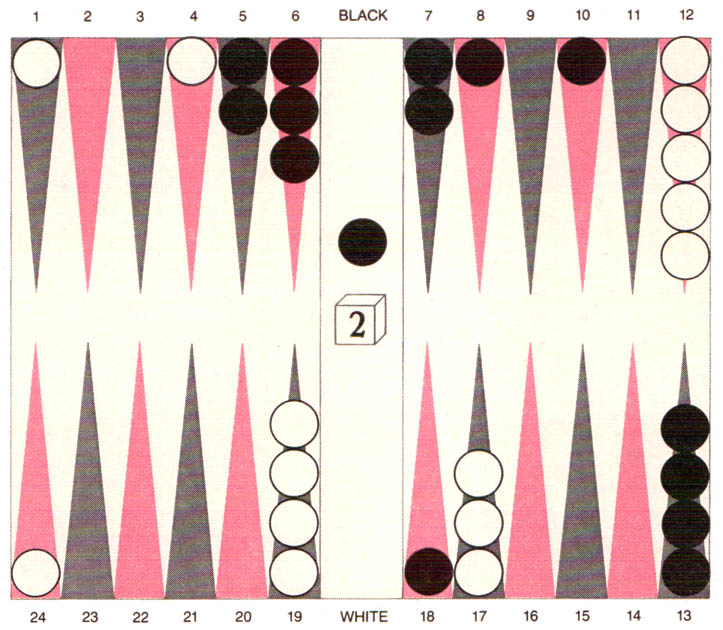
|
| BKG doubled in this position from the second game of the match. The double was a good one, and Villa declined it. The question of doubling comes down to deciding whether one’s position is too weak, too strong or just right. If the position is too weak, the opponent will accept the double. If it is too strong, he will decline, losing only the original stake and not twice the stake, which he could have lost if the double had not been offered and he had been gammoned. |
Villa got off to a good start in the third game. He built up a strong position and doubled at a time when it was appropriate for BKG to decline. The program accepted, however. Villa was now on his way to winning the doubled game, but through a series of unfortunate rolls he was forced to leave an exposed blot as he was bearing off his pieces. The program was not able to hit the blot immediately, but Villa was forced to leave another blot two rolls later. This time BKG got a good number, hit one of Villa’s pieces and went on to win by redoubling him when his position was hopeless. This made the score 5–0. The television room was now full of spectators, who groaned and cheered as the game swung back and forth between the combatants. It was like the semifinals and finals of the world championship, when the room was packed with aficionados who argued about which moves were best and which side was in the better position.
At this point I was quite pleased with the way things were going. In my fondest dreams I might have hoped for five or six points in a losing contest. Yet here we were, leading 5–0 with an excellent chance of winning the match. I had worried that an expert might be able to play in some strange way that would entice the program into unusual situations where it would blunder seriously. Of course, a great deal had been done to try to prevent this possibility. It was nonetheless on my mind, although it never came about.
In the fourth game Villa quickly got an advantage and doubled early, hoping to recoup some of his losses if he could go on to win. The BKG program, however, chose to play it safe and keep its dominating lead by declining the double. It was a close decision whether or not the program should have declined. The score was now 5–1, and the crowd in the television room was ready to see Villa make a comeback.
The fifth game was the most interesting and fateful of the match. BKG played most aggressively in the early stages, and as a result two of its pieces were hit and sent back. The program made the best of this loss of time by establishing a back game: an exceptionally strong defensive formation in which two defensive points are held in the opponent’s home board. This meant that Villa’s victory in the game, if there was to be one, would be a long way off. The central concept of a back game is to lure the opposing pieces forward as fast as possible in the hopes of eventually hitting a piece and sending it back. For this strategy to succeed it is necessary to have a good defensive position with one’s own pieces not advanced too far. Otherwise it will not be possible to contain the piece that is sent back.
Both sides played well for several moves, and then BKG rolled an unfortunate double five in the position shown in the illustration below. As a result the program had to advance its pieces faster than it would have liked. It showed its excellent command of the position by playing two pieces from the 8 point to the 3 point and one piece from the bar to the 15 point, leaving three blots that could be hit. Of course, the program would not have minded at all if the blots had been hit; that would have slowed the advance of its own pieces and would have put it in a better position to hit one of Villa’s pieces. Moreover, the blots were ideally situated to obstruct the mobility of Villa’s forces, which could not afford to be hit because the program had already achieved a good defensive formation.
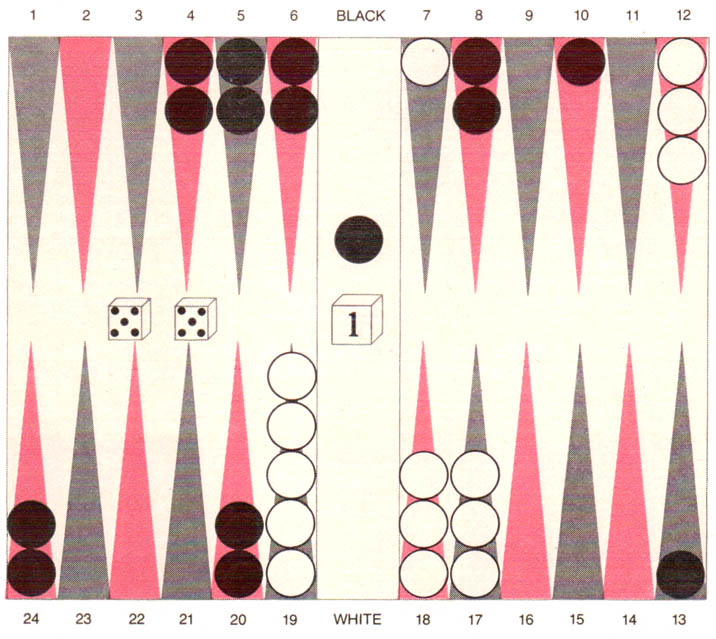
|
| BKG rolled two fives in the fifth and final game of the match. The program played 8/3(2) and bar/15, leaving three blots. If the blots were hit, BKG would have more time to reinforce its back game: the holding of the 24 point and the 20 point in Villa’s inner table. |
Several moves later BKG had to play a five and a one in the position shown in the illustration below. The obvious play was to move a piece from the 13 point to the 7 point in the hope that this piece would be hit as Villa’s last piece on the 2 point tried to escape. If the piece had been hit, the program would have had more time to plan its defense. The program rejected this move, however, for the sensational one of moving a piece from the 13 point to the 8 point and a piece from the 3 point to the 2 point.
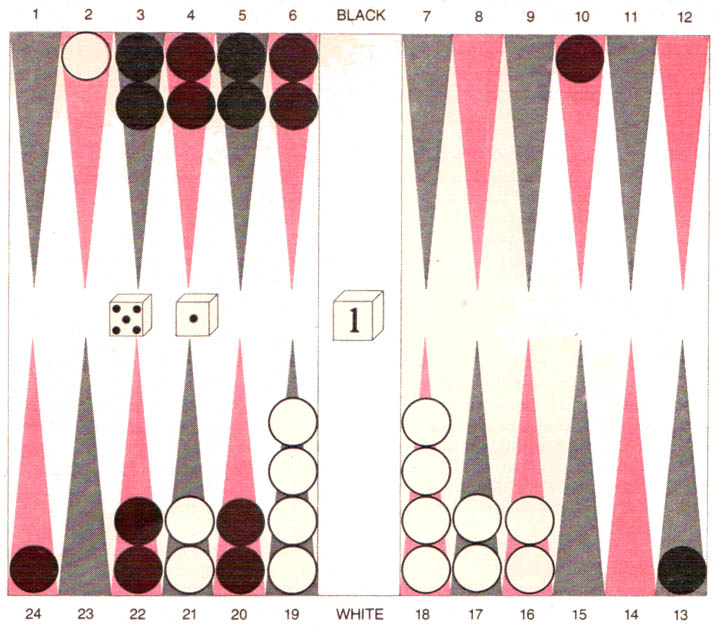
|
| BKG rolled a five and a one in this position in the last game. The program made the sensational play of 13/8 and 3/2. If any of BKG’s blots were hit, it would have more time to build up its back game. On the other hand, if they were not hit, it would be able to make points in its home board, making it more difficult for Villa’s piece to come back in and then escape. |
Although this move destroyed part of BKG’s defensive formation, it was an aggressive double-edged continuation that was judged to be correct by the watching experts. The conception is as follows. If Villa hit one or both of the blots in BKG’s home board, then BKG would gain time to improve the effectiveness of its back game. On the other hand if the blots were not hit, BKG would have a chance to establish an even stronger defensive position, making it more difficult for Villa’s back piece to escape from the program’s pieces that contained it. In essence BKG’s outstanding play gave it not one but two ways to win. Nevertheless, the play was risky, and Villa, with much to gain and little to lose, doubled and BKG accepted.
Villa immediately hit a blot as he brought in his piece and started moving his forces home. The program now rolled another two fives, again forcing it to advance its pieces faster than it would have liked. A few moves later came another critical moment. BKG had to play two twos in the position shown in the illustration below. Here a player who is not an expert might be tempted to maintain his back game by playing a piece from the 22 point to the 20 point and two pieces from the 6 point to the 2 point and the 4 point. BKG realized, however, as most experts would, that a back game is useless without a strong home-board position. In fact, it risks being gammoned.
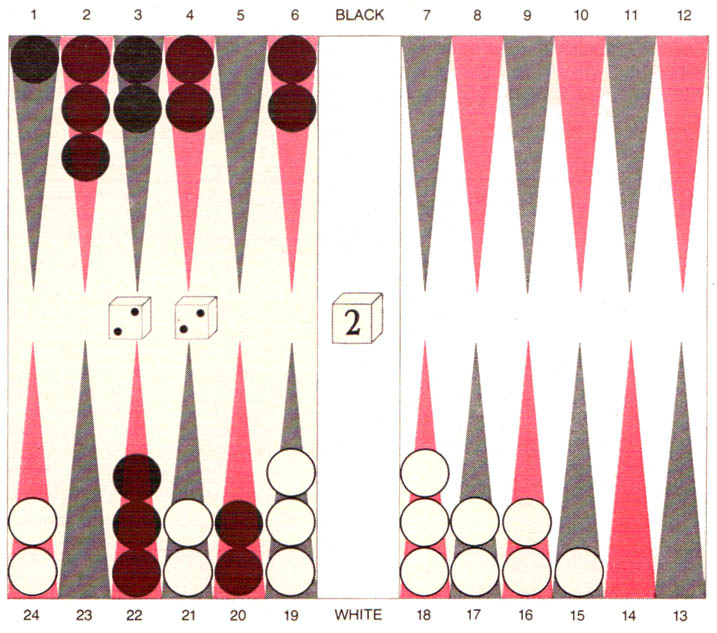
|
| BKG rolled two twos in this position in the final game. By making the play 3/1, 22/20(3) the program correctly abandoned its back game and started moving its army of pieces home, in the hope of not getting gammoned. Although the program was the underdog in the race, it got lucky rolls and ended up winning the doubled game and the match. |
Therefore BKG moved a piece from the 3 point to the 1 point and three pieces from the 22 point to the 20 point. This play abandoned the back game and started a race for the home board in order to limit the program’s losses to a doubled game. Soon BKG was rewarded unexpectedly for its good play. In the next 12 turns for each side the program’s designated dice thrower outrolled Villa by 31 pips (4.3 pips is the standard deviation for a single roll), achieving a position in which it had about a 20 percent chance of winning. At that moment out of its dice cup came two sixes, which enabled the program to take off its last four pieces, winning the game and the match.
I could hardly believe this finish, yet the program certainly earned its victory. There was nothing seriously wrong with its play, although it was lucky to have won the third game and the last. The spectators rushed into the closed room where the match had been played. Photographers took pictures, reporters sought interviews and the assembled experts congratulated me. Only one thing marred the scene. Villa, who only a day earlier had reached the summit of his backgammon career in winning the world title, was disconsolate. I told him that I was sorry it had happened and that we both knew he was really the better player.
Several weeks later I analyzed the games in some detail at Carnegie-Mellon. There was no doubt that BKG 9.8 played well, but down the line Villa played better. He made the technically correct plays almost all the time, whereas the program did not make the best play in eight out of 73 nonforced situations. Only one of these mistakes, however, gave the program any trouble. An expert would not have made most of the errors the program made, but they could be exploited only a small percent of the time.
BKG 9.8 shined brightly when it came to exercising imagination. Someone who did not know whether the program was playing White or Black might have thought it was the human competitor who was making the sparkling plays and the machine the stodgy ones. In the match the dice had the final say, and they spoke for BKG 9.8.
The BKG program will now be developed in two areas. First, I plan to build more knowledge into it. Second, I want to make it into a teaching program that will ultimately be able to perceive its own weaknesses and modify itself to correct them. The first task will take time but does not seem to be too demanding. BKG 9.8 already seems to know most of what is important in backgammon. Although the accuracy of its knowledge is high, there are places where the values of the application coefficients of functions can be improved somewhat and where additional knowledge could be beneficial. My co-workers and I are currently proceeding along these lines.
|
| Dialogue between human player and BKG will be possible in the future. The human player will select his questions from a list, and the program will formulate its answers by examining its own knowledge base and the set of possibilities in the current game position. |
There are many problems of backgammon such as the correct way of bearing pieces off the board that can be solved completely by numerical analysis with the aid of computers. One of my students has developed a complete data base for all positions with 15 pieces or fewer in the home board. The data base provides the expected number of rolls (accurate to five decimal places) that are required to bear off all the pieces. Given this information, it is possible to determine the best move for any dice roll in any bearing-off position. The data base, however, has 54,000 entries, so that would be wasteful of computer resources to keep it in the program. Yet it seems possible to develop a few rules that would incorporate all the bearing off knowledge. We are now in the process of developing a program that will generate its own rules and test and modify them until it eventually homes in on a small set of rules that will capture all the information in the data base. These rules will then be included in the BKG program.
Another problem that is solvable is the one of when to double. In the final analysis doubling comes down to deciding whether your position is too good to double, not good enough or just right. The crucial issue is how the position will have changed by the next time you have a chance to double. Since 21 different rolls are possible for each side before the next opportunity arises to double, 441 possible situations must be considered, assuming of course that all of them can be evaluated correctly. Nevertheless, it is usually possible to organize the situations into groups, each of which can be evaluated. If it turns out that your position would be too strong to double at the next opportunity for most of the 441 situations, then you should do so immediately. On the other hand, if the chances are that your opponent would accept a double now as well as the next time, then you should wait, because he might get lucky and roll good numbers as you roll bad ones. Expert human players approach doubling in much the same way that BKG will. If the program gets accurate inputs to its doubling equations, however, it should be able to outclass human competition in this phase of the game.
Situations sometimes arise in backgammon for which there are no well-developed models. These situations are usually referred to as situations requiring judgment. The program does quite well in this domain because of the success of the SNAC functions. It can nonetheless be improved in several places. I plan first to generate a large number of similar situations requiring judgment and then to tune and augment the affected functions until they yield the correct response in every case. This task could be a painstaking one that would be better done automatically, but I do not yet know how to do it that way.
It seems SNAC functions are the proper means of capturing the characteristic that human beings call judgment. They make it possible to respond to small changes in stimuli with small changes in behavior, and this is exactly what judgment (as opposed to logical deduction) is about. I think SNAC functions could be exploited successfully in computer applications ranging from aesthetics to everyday decision making in business. In any reasonable implementation it will of course be necessary to identify the important variables and their interactions and to tune the resulting functions.
The next five years should see remarkable advances in computer game playing. The current era of powerful game-playing programs began in July, 1976, when Chess 4.5, developed by David J. Slate and Lawrence R. Atkin of Northwestern University, won a tournament of Class B chess players in California. (On the official ranking scale Class E goes from 0 to 1,199, Class D from 1,200 to 1,399, Class C from 1,400 to 1,599, Class B from 1,600 to 1,799, Class A from 1,800 to 1,999, expert from 2,000 to 2,199 and master from 2,200 on up. The median rating of all U.S. tournament players is 1,362.) Since then Chess 4.5 has won the Minnesota Open Championship and has beaten experts and masters at “blitz” play (where each side has five minutes for the entire game).
Another strong chess program is Bell, developed by Ken Thompson and Joe Condon of Bell Laboratories, which incorporates special hardware specifically designed to carry out chess calculations. Soon it will be upgraded to conduct tree searches of many millions of nodes within the time limit of three minutes per move, a search that staggers the imagination. When the knowledge of Chess 4.5 is combined with the upgraded hardware of Belle, the program will, I am confident, play chess at the master level. SNAC functions may even help the program to develop a greater sensitivity to what is important in a given position.
Things look even brighter for computer backgammon. My program plays at the Class A, or advanced intermediate, level. When the improvements I have mentioned are introduced, I think the program will play all stages of the game at an expert level and will be able to do certain things better than any human competitor could in a short period of time without any mechanical or memory aids. At that point it should be difficult for the best players in the world to beat the program. I hope to eventually make BKG into a learning program that will get stronger by studying its own games.
Many people consider games such as backgammon and chess to be essentially frivolous. The results achieved in computer game playing, however, are certainly comparable to anything else that has been done in the field of artificial intelligence. The work on computer chess has led to major progress in techniques for searching a tree with many nodes and for breaking down a task for parallel computation. And the work on computer backgammon has led to better ways of organizing knowledge and making judgments.
BIBLIOGRAPHY
|
THE AUTHOR Hans Berliner is a senior research computer scientist at Carnegie-Mellon University and the holder of the permanent title Grandmaster of Correspondence Chess. After being graduated from George Washington University in 1954 with a bachelor’s degree in psychology he worked in the field of human factors for seven years until he decided to become more involved with computers. From 1961 to 1969 he worked in the Federal Systems Division of the International Business Machines Corporation, helping to develop large data-processing applications for the Federal Government. In 1969 he decided that he was more interested in research topics associated with computers, principally artificial intelligence, and went to Carnegie-Mellon, where he obtained his Ph.D. (in computer science) in 1975. By 1969 he had played on the U.S. Olympic chess team, had won the U.S. correspondence-chess championship the three times he tried for it and had won the international correspondence-chess championship (in 1968). Berliner stopped playing chess in 1969. |
![]()
|
| Articles by Hans Berliner |
|
| Articles on programming backgammon |
|
| Match transcript |
|
Return to: Backgammon Galore |
|