Introduction In this article, I will assume that you have read The Ash Dalvi 13 Count (Part 1). In Part 2, I will focus on how to include checkers within the home board into your 13 count. In Part 1, I discussed 2 ways that some of the home board checkers could be included into the count (See Position B and D below).   Position B. Two checkers equidistant from your bar counts as one 13.   Position D. Two opposite checkers + 1 pip equals 2 sets of 13. However, these 2 positions will not always get all the home board checkers into your count. Home board checkers When I started using this method, I just added home board checkers on at the end either using Jack Kissane's cluster counting method or by adding 1 or 2 checkers on low points at the end. The idea of the 13 count system was to avoid adding big numbers and several sets of multiplication and this was achieved in Part 1. In part 1, I showed you how to get all the checkers between the 24 pt and the 7 pt into your 13 count. Note that there are only 4 very simple positions to remember to account for all of these checkers. This is arguably an improvement on traditional cluster counting methods. You can always count the checkers on high points into a 13 count. However, if they are not situated in convenient positions, they can be difficult to incorporate into a traditional cluster count. In addition, sometimes, I simply want to know who is ahead in the race. In these situations, I am happy to rely on a 13 count without corrections if there is a difference of two 13s. For this reason, I have explored a couple of methods of incorporating home board checkers into the 13 count. Method 1.  Memorising corrections while maintaining symmetry If you are better at memorising numbers than patterns, this method may suit you better than Method 2. I use the following positions and memorise the corrections.   Position 1a. (2 checkers on the 6 point) 1 set of 13 and a correction of -1 pip.   Position 2a. (2 checkers on the lowest 3 points) 1 set of 13 and a correction of -1 pip.   Position 3a. (2 checkers on the 5 and 6 points) 2 sets of 13 and a correction of -4 pips.   Position 4a. (3 prime on the highest points) 2 sets of 13 and a correction of +4 pips.   Position 5a. (4 prime on the highest points) 3 sets of 13 and a correction of -3.   Position 6a. (5 prime on the highest points) 3 sets of 13 and a correction of +1 pip.   Position 7a. (Closed board) 3 sets of 13 and a correction of +3 pips. Method 2.  Memorising unsymmetrical positions without having to make corrections If you are more comfortable memorising patterns than numbers, Method 2 may be more useful to you.   Position 1b. (2 checkers on the 6 point and 1 on the 1 point) 1 set of 13.   Position 2b. (2 checkers on the lowest 3 points plus 1 one extra on the 1 point) 1 set of 13.   Position 3b. (2 checkers on the 5 and 6 point and 1 on the 4 point) 2 sets of 13.   Position 4b. (2 checkers on the 6, 4 and 3 points) 2 sets of 13. Usually when your opponent makes your 5 point, it is considered bad. However, on the bright side, it can make pip counting easier. That thought helps me to remember this pattern.   Position 5b. (4 prime on the highest points with an extra checker on the 3 point) 3 sets of 13.   Position 6b. (4 on the 6 point and 3 on the 5 point) 3 sets of 13.   Position 7b. (3 on the 5 and 6 points and 2 on the 3 point) 3 sets of 13. 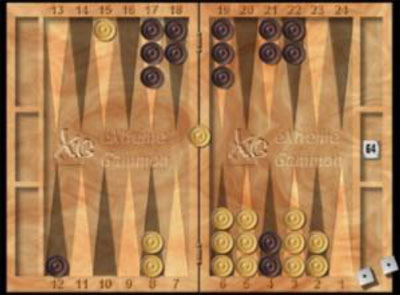Example 1 White's 13 Count Step 1.  Figure out your strategy as to how you will count the 13s The 3 checkers on the 13 pt can be counted as normal 13s as in Position A (Part 1). 13 pt (Position A) -- Three 13s The 8 in the home board are 3 sets of 13 (Position 6b). Position 6b -- Three 13s The 4 checkers in white's outer board will be counted as 4 sets of 13 (Position A Part 1). Four 13s. The reason I am counting them as 13s is because I can know that the correction for an 8 pt checker is -5. Because there are 4 checkers, the correction will be simple -20 (for the 4 checkers) + 2 (for the checker on the 10 pt). I could have counted them as equidistant from the bar (Position B Part 1). However, the mental shifts look more time-consuming using that method. The 13 count is 10. 10 x 13 = 130. Step 2.  Mental shifts 13 pt (Position A) -- no shift needed. The four checkers in my outer board 130 - 20 + 2 (Position A) = 112. Checkers in my homeboard (HB 6b) - no mental shifts required. This gives a total of 112 pips. Black's 13 Count Step 1.  Figure out your strategy as to how you will count the 13s The 2 checkers on the 13 pt can be counted as normal 13s as in Position A (Part 1). 13 pt (Position A) -- Two 13s The 3 on the 6 pt, 2 on the 7 pt and 1 on the 8 pt can be counted as equidistant from the bar (Position B, Part 1). Equidistant from the bar (Position B, Part 1) -- Three 13s. The checker on the 24 pt can be counted as two 13s (Position C, Part 1). Two 13s. The remaining 6 checkers on the 3, 4 and 5 pts can be counted as two 13s (Position 4b). Two 13s. The 13 count is 9 -- 13 x 9 = 117. Step 2.  Mental shifts 13 pt (Position A) -- no shift needed. The checker on the 24 pt (Position C, Part 1) 117 -- 1 (for 1 checker) -- 1 (for it being on the opponent's 1 pt) = 115. The 6 checkers that are equidistant from the bar (Position B, Part 1) + 1 for the checker on the 8 pt. 115 + 1 = 116. The 6 checkers in the home board (Position HB 4b); the 2 checkers on the 5 pt need to be moved to the 6 pt to match Position HB 4b which is 2 pips. 116 - 2 = 114 which is the total pip count. Example 2 Let's start with Black's pip-count this time. Black's 13 Count Step 1.  Figure out your strategy as to how you will count the 13s The 3 checkers on the 13 pt can be counted as a normal 13 as in Position A (Part 1). 13 pt (Position A) -- One 13. The 2 checkers on the 21 pt can be counted as two 13s each (Position C, Part 1). 2 checkers (Position C) in opponent's home board -- Four 13s. Six checkers in black's homeboard (2 on the 6, 5 and 4 pts) can be counted as 2 sets of 13 (Position 4b). Position 4b -- Two 13s. The remaining 6 checkers (3 on the 8 pt, 2 on the 7 pt and 1 on the 6 pt) can be counted as equidistant from the bar (Position B, Part 1) -- 3 sets of 13. Three 13s. The 13 count is 10. 10 x 13 = 130. Step 2.  Mental shifts 13 pt (Position A) -- no shift needed. The two checkers on the 21 pt need correcting 130 -- 2 (for the number of checkers) -- 8 (for each being on the opponent's 4 pt) (Position C, Part 1) = 120. Six checkers in black's homeboard (2 on the 6, 5 and 4 pts) (Position 4b) -- no correction. The remaining 6 checkers ( 3 on the 8 pt, 2 on the 7 pt and 1 on the 6 pt) counted as equidistant from the bar (Position B, Part 1). The 5 checkers on the 7 and 8 pt need to be shifted 1 pip in for the checkers to be symmetrically equidistant from the bar -- 5 pips. 120 + 5 = 125 which is the total pip count. Now white's pip-count. White's 13 Count Step 1.  Figure out your strategy as to how you will count the 13s The checkers on the 15 pt can be counted as normal 13s as in Position A (Part 1). 13 pt (Position A) -- One 13. The 2 checkers on the 8 pt can be paired with the 1 checker on each the 5 and 6 pt to be counted as equidistant from the bar (Position B, Part 1). Equidistant from the bar (Position B, Part 1) -- two 13s. The other 9 checkers in white's home board can be counted as a 4 prime with an extra checker as in Position HB 5b -- three 13s. The checker on the bar can be counted as two 13s (Position C, Part 1). Two 13s. The 13 count is 8 -- 13 x 8 = 104. Step 2.  Mental shifts 13 pt (Position A) -- the checker on the 15 pt needs to be moved 2 pips be on the 13 pt. 104 + 2 = 106. The checker on the bar (Position C, Part 1) 106 -- 1 (for 1 checker) and 0 (for it being on the bar) = 105. To get the checkers on the 8, 6 and 5 pts equidistant from the bar (Position B, Part 1), you can move the 6 pt checker forward by 1 pip. 105 + 1= 106. In order to get the remaining 9 checkers in white's home board into Position HB 5b, you need to move 2 checkers on the 2 pt and 2 checkers on the 3 pt back by 1 pip (ie by a total of 4 pips). 106 - 4 = 102, which is the total pip count. That was quite easy to do and it didn't take much time. However, I included this position deliberately to demonstrate a position that I would definitely change counting method. Anyone who is familiar with cluster counting will immediately see that if you remove a checker from black's 6 pt, the remainder of the checkers on black's home board will add up to 40 pips. It is a 5 prime position with 1 checker either side of the 4 pt instead of actually being on the 4 pt (ie the middle pt which is 4 x 10 = 40). In addition, if you are used to counting in 10s, you will know that the checker on the bar and the checker on the 15 pt will add up to 40. So all you have to do is add the 2 checkers on the 8 pt and the checker on the 6 pt to 80 to get 102. Similarly, in Example 1, for black's pip count, I would count the 10 checker that make the 5 prime as 50 pips and just include the remaining checkers into my 13 count. It is important to be flexible when pip-counting. If the layout of the checkers is more amenable to another pip-counting method, you should switch or combine methods. Which Method is Best? The method you choose depends on how your mind works and the layout of the checkers in a given position. After practicing including home board checkers into my 13 count, I've decided that an eclectic approach to pip-counting is best for me. I use both of the above methods as well as traditional cluster counting methods and sometimes I just add the pips on low points onto my total at the end of my 13 count. The method is flexible because you adapt it in accordance with how the checkers are situated. Whatever strategy of counting you see first is probably the best strategy. It can be advantageous including home board checkers into the 13 count if all you want to know who is ahead in the race. As mentioned earlier, if you are two 13s ahead, you can be fairly comfortable about being ahead in the race. An exact pip count may not be necessary. For the home board checkers, I would simply advise you to use the strategy to pip-count that is easiest for you. I wouldn't say that the 13 count is particularly an improvement on other methods for the purposes of counting pips on low points. As mentioned earlier, the purpose of this technique was to reduce the addition and multiplication of large numbers and count the checkers on high points easily. For most people, the checkers in the home board aren't difficult to count anyway. There are many pip-counting methods. They all have some advantages and disadvantages. Some of the disadvantages of a system may only be disadvantageous to some people but not to others. I find this method suits me because I have a tendency to make mistakes when I add large numbers together and to forget one number while calculating a second number to add to it. I suggest practicing with the techniques in Part 1 first and then include the techniques in Part 2.

See also:  Other articles on pip counting.

Return to:  Backgammon Galore