Introduction
Snowie is not really one robot, but many. The reason is that there are several optional parameters which can be set by the user. Jellyfish also has paramaters, but few compared to Snowie. Before showing the time impact of these various parameters, let's take a look at them and explain their meaning and implementation. (Much of this information can be found in Snowie's extensive help-file.)Definitions
1. Ply. As with Jellyfish, there are three ways to set Snowie's lookahead ability. 1-ply means Snowie uses just the position available and its neural-net (brain). It does not compare the positions after various diceroll sequences. At a 2-ply setting, Snowie looks at the (opponent's) 36 reply rolls, records the way it would play each of these 36 numbers, and then combines the results (1/36 * subsequent equity for a given roll, summed over the 36 possible rolls) and makes its decision. Naively this should take 21 times as long to accomplish as 1-ply. Full 3-ply means Snowie looks at roller's 36 responses to each of opponent's 36 rolls and weighs them accordingly. Again, this should take considerably longer than 2-ply, and it does.If Snowie takes longer at deeper plys, why bother wasting time? The bottom line is that Snowie is 'smarter' the deeper it looks ahead. How much smarter are the higher plies? That is what part III of this project will hopefully tell us.
2. Truncation. To shorten the time of a rollout, you can tell Snowie how many dicerolls per trial, and to then evaluate the position and go on to the next trial. Basically you get random dice for the number of rolls indicated (truncation depth) and then an evaluation. Although this kind of rollout in general will give more reliable results (that is, indicates closer the 'true' equity of the original position being rolled out) than mere evaluations, it's not as robust as full (untruncated) rollouts. It's still vulnerable to Snowie's imperfect evaluation function. For checker play rollouts (where you are trying to find the best checker play among several candidates), truncated rollouts probably lead to reasonable results, based on the concept that the evaluation function error (which occurs at the end of the number of specified rolls) has a similar magnitude and direction for each of the candidates. For cube decision rollouts, especially complicated positions (for example, backgames), the absolute value of the result determines the proper cube action, so untruncated rollouts are likely to be the most reliable.
3. Bearoff database usage. Snowie has a built in bearoff database. This file contains bearoff positions and when both sides are put together, an accurate estimate of each player's game winning chances result. By stopping and evaluating a rollout once positions in the database are reached, considerable time savings result. I know of no reason not to use this option for any rollout to be performed.
4. Live cube. Snowie has the capability to use a doubling cube during the rollouts. This is true for both checker-play and cube-play rollouts. When performing this kind of rollout for a money game, the user can tell Snowie a maximum cube level. The purpose is to prevent one or even a few games with very large cubes dominating the results. At the maximum level the game is stopped when a certain equity threshold (also user specified) is reached. For matchplay this maximum cube level option isn't available since the finite matchlength effectively limits the cube's hightest value.
When performing a live-cube rollout, Snowie goes through all the evaluation of cubeless rollouts, but in addition it also keeps track of doubles, takes, and passes. As a result, live-cube rollouts take longer, although as will be seen later, specifying a smaller ply for the doubling decisions than for the checker play decisions, very little time is added.
5. Search space. Typically Snowie must evaluate many different candidate plays. At 1-ply this doesn't take long, but at higher plies the number of positions to be considered grows precipitously. By specifying a 'search space' value (there are six choices), Snowie limits the number of candidates in two ways. First it looks to see how much difference in equity there is between plays at the lower ply. If that difference is small it will continue to higher plies for the competing (close) candidates. In addition, even if many plays are close, there is a maximum number it will continue looking at to higher plies. At 2-ply, the maximum number of candidates to be considered can be set between 3 and 13. For a 3-ply rollout, in addition the number of candidates considered is somewhere between 2 and 7, depending on the user's choice of search space. Snowie coins these spaces 'supertiny' through 'huge'. The six titles are sufficiently descriptive.
6. Speed. To me this parameter could have been better named. I would prefer "chainsaw size" or something equally descriptive! This setting only applies at the 3-ply level. The structure of candidate plays at 3-ply grows like a tree. For Snowie to look at all of the leaves of this tree would take a considerable amount of time. The 'speed' parameter tells Snowie where to trim the branches of this tree so as to quicken the rollout. There are five speed settings (20%, 25%, 33%, 50%, 100%) but the speed of the rollout is inversely related to these numbers. That is, 20% trims the tree closer to the trunk and runs fastest. A 100% speed setting takes the most time.
7. Checker play according to score. Although the name of this parameter implies matchplay rollouts, this can be checked for money games. The reason is that, when playing with a cube, the best play may be different than when cube turns aren't possible. In order for this option to be used, a live-cube must be active, even if (based upon the matchscore), the cube is dead. In principle, when making its evaluation, Snowie adjusts for the different cube locations and gammon-prices that the matchscore inflicts. For example, the best play at double-match-point (when neither player can gain from a gammon) is sometimes different from the top choice at money play. The Snowie Helpfile warns that selecting this parameter increases rollout time by a factor of 3! We'll see below if our experiments back up that claim.
Strategy of Data Taking
If our goal was to measure times for every possible combination of rollout settings, the task would be formidable indeed. For cubeless money play alone and a fixed number of trials (for example, 36, as was used in most of this study), there are 200 1-ply, 1200 2-ply, and 6000 3-ply possible setups! The data presented here in graphic form represent only 190 rollouts. Because most computers used today are fast enough to run the more reliable 2- and 3-ply rollouts, I concentrated on these levels. In addition, because the 'speed' parameter is applicable only for 3-ply, most of my tests were done at that level.I used a Pentium II-233 exclusively for this study. Part I (last month) showed how runtimes relate to CPU speed. At the end I will give parameterized equations for various conditions (including CPU speed), but the results below should be proportional to the performance on other CPU's. In particular, if a setting change in the data for this study predicts a given time factor increase, that should also occur on a different CPU. For example, for a cubeless 3-ply rollout with speed setting of 100%, going from a supertiny search-space to a small search-space caused the rollout time to double in this study. That same factor of two increase in time should occur for similar rollout settings on a faster computer.
In all 190 rollouts, the same position and initial diceroll were used: the standard opening game setup, a 62 opening roll, and three candidate plays (24/18, 13/11; 24/16; and 13/5). The bearoff database was activated. A random seed (chosen by Snowie) was also used for each rollout. You will notice in the graphs presented below that there is some 'jitter' in the data which is mostly a result of statistical fluctuation in runtimes due to the small sample size (36 trials for each candidate) used to keep the experiment manageable.
Results of Parameter Variation
In all plots, the vertical axis shows the runtime (in seconds) for the rollouts presented. The horizontal axis (and multiple curves, when shown) represent the different parameter settings.
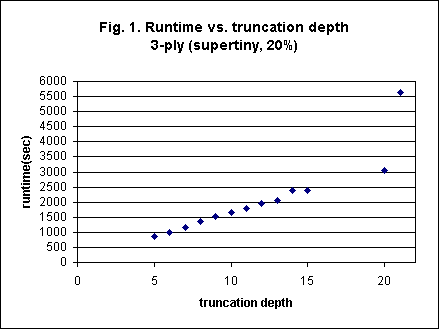
Figure 1 shows the effect of truncation depth. The data represented here were taken at the 3-ply level without cube. The searchspace and speed parameters were set at their minimum values (supertiny, 20%). The truncation value was varied from 5 to 15 (rolls) in increments of 1. Two more truncation settings -- 20 and untruncated -- were also tested. On the plot, the rightmost (high) point is the untruncated result. A nice linear relationship can be seen. This makes sense. If you require Snowie to toss twice as many dicerolls before truncating (evaluating), it takes twice as long. It can also be seen that the untruncated datapoint represents about 35 dicerolls (before reaching the bearoff database).
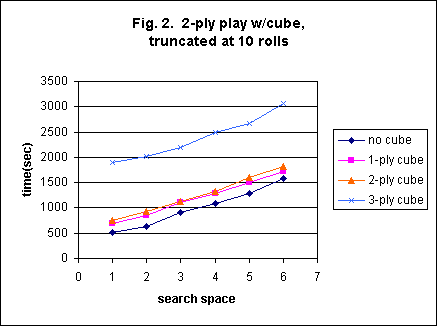
All of the 2-ply (truncated at 10 rolls) results of this study can be seen in figure 2. Two parameters were varied here: cube setting and search-space. (For all figures from here on, I have converted searchspace to numeric values as follows: supertiny = 1, tiny = 2, small = 3, medium = 4, large = 5, and huge = 6). Note that the difference in runtime between two different cube levels is independent of search-space. There is overhead for adding a doubling cube to the rollout, and the amount of overhead depends upon the ply level used in determining the cube decisions, but not on the choice of search-space. You will also see that there is a small overhead going from no cube to 1-ply cube, but very little difference between a 1-ply cube and a 2-ply cube. Finally there is a large increase in runtime when cube decisions are based upon 3-ply analysis.
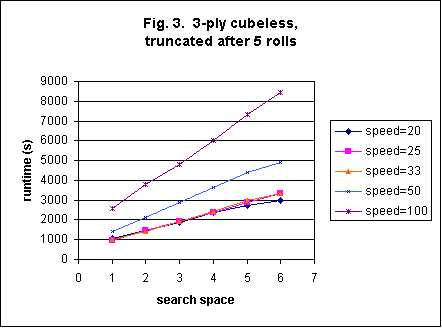
Figure 3 shows the runtime dependence on search-space and speed for 3-ply cubeless rollouts truncated at 5. This is the 'bread-and-butter' plot of this study, since 3-ply rollouts are the power of Snowie, and searchspace and speed settings make a significant difference in 3-ply rollout runtimes. Here it can be seen that the first three speed levels give almost the same runtime. This probably means that, at least for early game decisions, the tree pruning algorithm isn't much different for 20%, 25% and 33% speed. Therefore, it makes sense that one might as well run 33% since it doesn't result in an increase in CPU time.
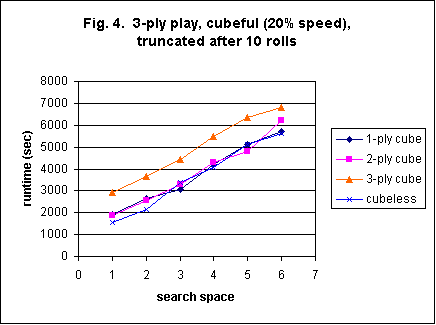
Figure 4 illustrates the effect of adding the cube to 3-ply (20% speed) rollouts truncated after 10 dicerolls. As was seen with 2-ply play, the cube only adds overhead when it is used at 3-ply. Even cubeless runs no faster than a 2-ply cube when 3-ply play is implemented. As was also noted for 2-ply, the introduction of a 3-ply cube adds a constant time increase, independent of searchspace.
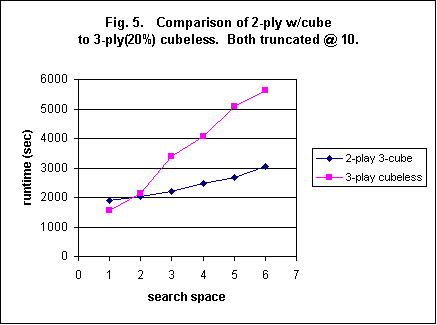
Although most of the emphasis of this study has been on the 3-ply setting, it is interesting to compare the slowest 2-ply play settings (with a 3-ply cube) to cubeless 3-ply play (speed setting 20%). Figure 5 shows such a comparison. Interesting that for a supertiny setting, 3-ply cubeless is faster. For a tiny searchspace, the two different rollouts take about the same amount of time. But at higher searchspaces, 3-ply cubeless burns up more clock. This is another illustration of the fact mentioned earlier that the cube adds a constant time overhead, independent of searchspace.
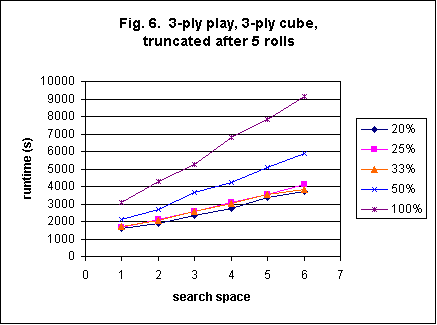
The longest (but likely the most reliable) settings are 3-ply play with a 3-ply cube. Figure 6 shows the affect of varying both the searchspace and the speed for these deepest levels. Note that once again, there is little difference between the time required for rollouts with the slowest three speed settings. After that, though, both the speed setting and the searchspace setting have a major impact on runtimes.
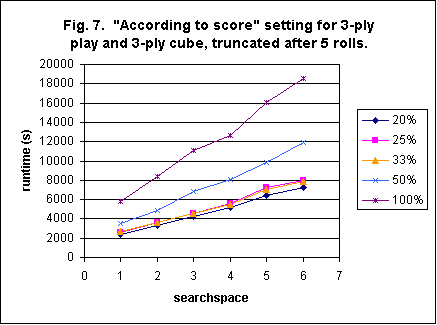
The ultimate in rollouts involves the "checker play according to score" (and cube position) setting. Figure 7 shows the runtimes when this parameter is used. By comparing figure 7 with figure 6, an increase of runtime by approximately a factor of 2 is evident. Note that this is not quite as large of a penalty of runtime as predicted in the Snowie helpfile -- a factor of 3 there. (Actually, for some positions, a factor of 3 may be the accurate number.) Still, doubling the runtime can be a serious time consuming decision and one should make sure this extra complication is warranted.
Equations for Predicting Runtimes
The data presented above has been combined to produce equations which express runtimes for the various parameter settings. For 2-ply lookahead, the formula isT2 = (ca/3)*(N/36)*(233/ps)*(tr/10)*(216*ss + ct) seconds
with the meaning of the variables: 'ca' is the number of candidate plays being rolled out, 'N' is the number of trials, 'ps' is processor speed (in MHz), 'tr' is truncation depth, 'ss' is searchspace (1 thru 6) and 'ct' is an overhead term which includes standard overhead and cube computation time. ct takes on one of the values [246, 441, 503, 1587] for [none, 1-ply, 2-ply, 3-ply] cube respectively.
For 3-ply rollouts, the expression is:
T3 = (ca/3)*(N/36)(233/ps)*(tr/5)*sf*(78.4 + 171*ss + 13.1*s + 10.1*s*ss + 500*cf) seconds.
Here 'ca', 'N', 'ps', 'tr', and 'ss' are defined above. 'sf' is the score factor and has a value of 2 when "checker play according to score" is used, 1 otherwise. 's' is Snowie's 'speed' setting (33, 50, or 100); 'cf' is the 'cube factor' and is 1 when a 3-ply cube is in use, and 0 otherwise. Note that although Snowie's 'speed' can be set at 20% and 25%, the data shown earlier indicate little difference between 20%, 25%, and 33% so in the parameterization, use 33% speed if running at either 20% or 25%.
These arithmetic expressions are meant as a guideline to help select parameters which will allow a rollout to be completed in an alotted time. Even for early game positions (for which they were derived), I wouldn't expect the predictions to agree better than 10-20%. For complicated positions, longer runtimes are probably to be expected while for simpler positions, shorter runtimes than the predictions are possible.
Part III—A Preview, and Call for Assistance
When I proposed this group project in January, I outlined three parts. The first was a study of the effect of different CPU's, and this work, thanks to the participation of several GoL members, was quite successful. (See the February issue of GoL.) Due to the many parameters which required systematic variation, I chose to perform the rollouts for part II myself. We now know the time impact of the various Snowie parameter settings. That, alone, is insufficient for the serious Snowie user, however. We don't yet know the impact, equitywise, in the various settings. For example, running the huge searchspace can be seen to increase the runtimes by a large factor. Is this extra effort reflected in more reliable results? If not, then we shouldn't waste the CPU-time, especially since we may not want to wait so long to get answers.I definitely can use (or, more strongly stated, NEED) help in this last part. I only ran 36 trials for each of 3 candidate plays for each rollout. We now want to run longer rollouts, especially for higher truncation levels. We need at least 10,000 (equivalent) games per position, and that is a bare minimum. More would be better.
In addition, this 3rd part is being opened to all robots, not just Snowie. Although I'd like to limit the position to the one used previously (standard opening, 62 roll, three most common candidate plays), I think it will be interesting to see the results arrived at by different robots. I've already received some gnu-backgammon data from Gary Wong, but more is needed, not only for that bot but for Jellyfish, Expert Backgammon, and ANY homegrown programs, for that matter.
Initially I'm going to ask contributors to choose their own (favorite) settings from the wide variety of possibilities and send the results to me. I'd like to see as much output (in terms of rollout results) as is made available. Please e-mail all results to me at bower@astro.indiana.edu. I have already received a few sets of Snowie results, and I'll thank all contributors by name in the final writeup, but I need more, More, MORE! Please contribute. Hopefully all of us can reap the collective rewards.