When Ralph Eskinazi and I were having dinner at The Mirage
in Las Vegas recently whilst attending the Las Vegas Open,
he asked me to explain the mathematics involved in doubling and take
decisions. I said it was quite complicated as it involved knowing the
match equities at various scores and then applying the formula:
Gain / (Risk + Gain)
Few of us could hold such numbers in our heads, I told
him, and do the mental calculations involved. He asked me to do an
article explaining this in more detail — so here goes.
First the match equities. Kit Woolsey produced a table to show
these. Others have slightly modified Kit's method so you will find
other tables that differ slightly from Kit's. I will use the one in
Robin Clay's Backgammon - Winning Strategies
(Page 131). Rick Janowski has provided a formula (Page 130) that is
accurate enough for most purposes and there are others available.
The 11 point match equity table below was compiled using Rick Janowski's formula:
Match Equity = 50 + ((D/85)/(T+6))%
where D is the difference between the scores of the leader and trailer and T
the number of points the trailer has to go. Adjustments have been made
to allow for the effect of the Crawford Rule at scores close to the
winning figure.
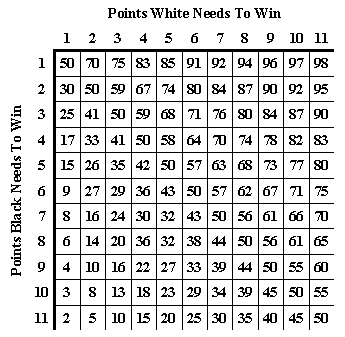Match Equity Table
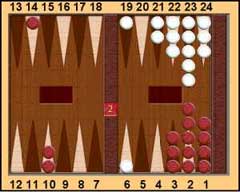
I will use the position below which Ralph had in a crucial match to explain the calculations.
 |
|
Black 7 (Ralph) White 5.
White on roll. Cube Action?
|
White is on roll and he doubled. Ralph dropped. I said it looked an easy take.
What does the mathematics suggest? The score of 7 to 5, to 9 points
is 2-away, 4-away. If Black drops it is 2-away, 3-away. Consulting the
match equity table gives Black's match winning chances as 59%.
- If Black takes and wins, the score is 9 to 6: 100% winning chances.
- If Black takes and loses, the score is 7 to 7: 50% winning chances.
- The Gain from taking is 100% − 59% = 41%.
- The Risk from taking and losing is 59% − 50% = 9%.
The take point is: Risk / (Risk + Gain) = 9 / (9 + 41) % = 9 / 50% = 18%
Stig Eide in an Internet article gave 20%.
Do you think, Ralph, that you can win from this position 18% (or 20%)
of the time? If so you should take. It’s a clear take. Snowie 3
confirms this giving Black 33% wins and it also says White, with an
equity of 0.467 should not have doubled.
You will find some other examples in Robin's book on pages 131 to 134. These pages were written by me at Robin's request.
Let us also look at the double from White's point of view. If
he did not double and wins the score is 7-6 (2 away, 3 away) with match
winning chances 41%.
- If he did not double and loses, the score is 8 to 5 (1-away, 4-away) = match winning chances of 17%.
- If he doubles and wins, the score is 7 to 7, 50% MWC.
- If he doubles and loses, the score is 9 to 5, 0% MWC.
- Gain is 50 − 41 = 9%. Risk is 17 − 0 = 17%.
Using the formula we have 17 / (17 + 9) = 17 / 26 = 65% approx. White does not have 65% chance of winning so should not double.
Going through such figures helps to build up our experience of
whether or not a position is a double or take. Most of us will not be
able to do these calculations at the table. I still think it is worth
noting critical positions, as did Ralph, and then analysing them. This
will sharpen your future judgements.
