|
| Mathematics of Backgammon |

I mentioned in Hyper Fun 02 that there is a mathematical way of counting the number of possible hypergammon positions. Here is an outline of how that method works. It starts with factorials.
Factorials
The factorial of a number n (written n!) is the product of the positive integers less than and equal to n. For example, 9 factorial is
Combinations
A simple and handy formula for counting things is the combination formula, which is:
| n! |
| m! × (n − m)! |
It tells you the number of ways m items can be selected from a collection of n items when the order you pick the items in doesn’t matter. For example, the number of different ways 5 cards can be selected from a deck of 52 is
| 52 |
| 5! × 47! |
Arrangements
Another handy formula tells how many ways a given number of checkers can be arranged on a given number of points. For example, how many ways can 2 checkers be arranged on 3 points? The answer is 6, and we can list the possibilities:
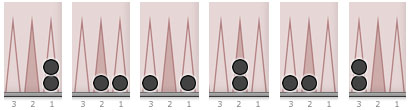
For more checkers and more points, there is a formula you can use to get this answer. The number of ways m checkers can be arranged onto n points is:
Bearoff Positions
Take, for example, the number of bearoff positions in backgammon. A “bearoff position” is where all off a player’s checkers are in his home board or borne off. The number of bearoff positions is
| 21! |
| 15! × 6! |
The “15” is the number of checkers we have to play with, and the “7” is the number of points those checkers can be arranged on. The reason we use 7 instead of 6 is that some checkers might be borne off, so we include the bearoff tray as one the points that a checker can be on.
Arranging Three Black Checkers
Here is another example. How many ways can you arrange up to 3 black checkers on a backgammon board?
There are 26 locations for those checkers — the 24 regular points, plus the bar, plus the bearoff tray. The number of ways of arranging 3 checkers on 26 points is:
| 28! |
| 3! × 25! |
This is a handy number to know and we will use it below.
Counting Hypergammon Positions
Okay, now we’re ready to count hypergammon positions. The easiest way to proceed is to break down the calculation into four parts:
- No points occupied by white. Suppose all of white’s checkers are either on the bar or borne off (so white has no checkers on points 1 through 24). There are 4 ways that white can arrange his 3 checkers this way. (He can have between 0 and 3 checkers on the bar, with his other checkers borne off.)
With no white checkers in the way, how many ways can black’s 3 checkers be arranged? We calculated the answer above, and it is 3,276. So the total number of hypergammon positions where white is not occupying any of the regular points is:
4 × 3276 = 13,104 positions - One point occupied by white. Suppose white occupies one of the regular points 1 through 24. There are 24 different points that could be. The other 2 white checkers can be in three locations (on the same occupied point, on the bar, or borne off). That is D(3,2) = 6 different ways to arrange the other 2 white checkers.
Black’s 3 checkers can be arranged on 25 locations (the 23 other points, on the bar, or borne off), so in D(25,3) = 2,925 ways. The total number of combinations is
24 × 6 × 2925 = 421,200 positions - Two points occupied by white. There are C(24,2) = 276 ways to choose the 2 points for white to occupy. The other white checker can be on either of those two points, on the bar, or borne off, that is, in 4 possible places. The black checkers can be arranged among 24 other locations (the 22 available points, or on the bar, or borne off), so in D(24,3) = 2,600 ways. The total number of combinations is
276 × 4 × 2600 = 2,870,400 positions
- Three points occupied by white. There are C(24,3) = 2,024 ways white can occupy 3 points with 3 checkers. The black checkers can occupy any of the other 21 points, or they can be on the bar or borne off. So black’s checkers can be arranged in D(23,3) = 2,300 ways. The total number of combinations is
2,024 × 2300 = 4,655,200 positions
Here are the final results:
| When white occupies 0 points | 13,104 positions |
| When white occupies 1 point | 421,200 positions |
| When white occupies 2 points | 2,870,400 positions |
| When white occupies 3 points | 4,655,200 positions |
| 7,959,904 positions |
This is the same answer we calculated by computer in Hyper Fun 02.
