|
| Backgammon Variants |

Unreachable Positions in Backgammon
A legal position in backgammon is a position that has up to 15 checkers for each side on the board, with no point having two checkers of different colors. There are 18,528,584,051,601,162,496 legal positions in backgammon.
Not all legal positions are reachable from the starting position. Here is an example:
|
| Stalemate position |
You will never see this position in a normal game of backgammon (unless somebody makes an illegal move). It is an example of a legal position that can’t be reached.
It is an interesting question how many unreachable positions there are in backgammon. Nobody really knows and I don’t think I’ve even seen an estimate of this number.
Unreachable Positions in Hypergammon
There are no “stalemate” positions in hypergammon, like the one above in backgammon. But there are positions that cannot be reached through legal play.
Unlike backgammon, where we don’t know how many positions are reachable, we can find out the number of reachable positions in hypergammon. I wrote a computer program to it, and it works like this:
The program maintains a table of the 7,959,904 legal positions and tries to see how many of positions can be reached. From the starting position, the program looks at the 15 possible opening rolls, tries every way of playing each roll, and marks in the table which positions are reached.
There are a total of 86 different positions that can be reached in one roll from the starting position. So those positions are marked as “found” in the table. From each of the 86 positions, the program looks ahead one more roll, tries all the possible plays, and marks as “found” the new positions it finds. This adds 12,343 positions to the total.
The program continues in this manner, each time looking ahead another roll and marking the new positions. Here is the output it produces:
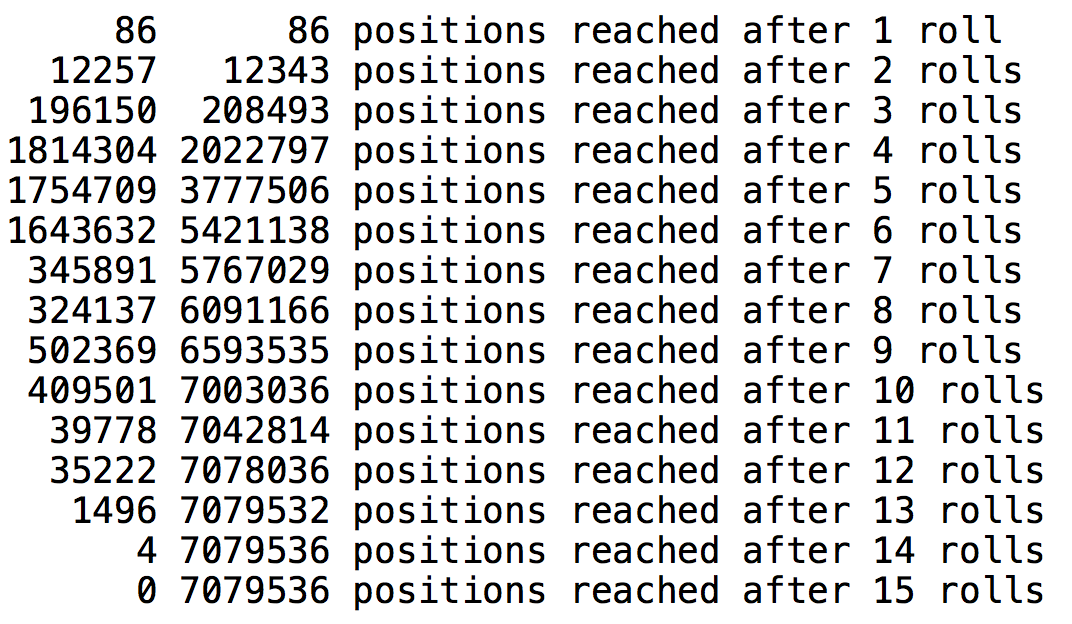
The first column of numbers is the number of new rolls found each time. The second column is total number of unique positions reached so far.
After 14 rolls, a total of 7,079,535 positions were reached. The fifteenth roll found no new positions. And that means we’re done — we have reached every possible position that can be reached in a game of hypergammon.
How Many Positions are Reachable?
In Hyper Fun 02, I asked what percent of legal hypergammon positions are reachable from the starting position and gave the following options: (a) 99.997%, (b) 98%, (c) 89%, and (d) less than 50%.
If you answered (c) 89%, then you are correct.
| Reachable positions | 7,079,536 | (88.94%) |
| Unreachable positions | 880,368 | (11.06%) |
| Legal positions | 7,959,904 | (100.00%) |
This surprised me a bit. I thought just about every legal position would be reachable somehow, that only a few weird cases would avoid having some path to them. But 11% unreachable positions is fairly substantial.
Does this 11% number have any implications for backgammon? Maybe backgammon has a similar ratio of unreachable positions. Or maybe there are many more or many fewer unreachable positions in backgammon. I don’t know.
A Hard-to-Reach Position
One thing that caught my eye from the output of the computer program above was that there are only four positions that take 14 rolls to reach. One of those positions is this one:
|
| Reach this position in 14 rolls |
Each side has two checkers on their own 8-point.
You can see why this would be a hard position to get to. Notice that both sides have one checker borne off already. That means at some point each side had all their checkers home (though obviously not at the same time), yet somehow their two remaining checkers are now back outside their home board. Not your everyday game!
Can you figure out how to get to this strange position? Can you do it in 14 rolls?
Postscript
After I posted the 8-point versus 8-point puzzle above, Nack Ballard suggested two other hard-to-reach positions. Can you find a sequence of rolls and moves that take you from the starting position to either of the positions below? (The second one is particularly tough!)
|
| Reach this position in 12 rolls |
|
| Reach this position in 10 rolls. (Either side may go first.) |

|
|

