|
| Mathematics of Backgammon |

Equity
“Equity” is the value of the current position in the game. You can think of it as the average amount you win or lose if you play out the same position many, many times.
We generally assume perfect play when we talk about equity — that on each turn the player makes the best possible move he can. What is that move? Why it’s the play that produces the highest possible equity.
But what if some positions don’t have a single defined equity? What if there is no such thing as “perfect play”?
This article is an amalgamation of posts to the Usenet group rec.games.backgammon in 1997. It ponders the question: Is equity defined in money backgammon?
The Tanenbaum Position
[Paul Tanenbaum, 1997.]
The diagram below should pique the interest of backgammon theoreticians. Its invention was motivated by the paper: “Optimal Doubling in Backgammon.” It is presented as a problem: What makes this position extraordinary?
Those without access to the aforementioned paper will find this a real challenge, though there are some contributors to this newsgroup who are evidently perspicacious enough to suss it out on their own.
I have since been informed that Bob Floyd published a position essentially identical in an obscure, now defunct, backgammon magazine several years ago. He therefore deserves recognition of first discovery. This posting is submitted for the edification of those unfamiliar with that article.
Do any other positions exist which possess the same property?
It should be noted that the Jacoby rule regarding an initial double may or may not be in effect; the conclusion is unaltered. Also, realize that it is quite legal. [However, see this note below.]
|
|
Money play: Black on roll. (Or white on roll — it doesn’t matter!) |
Gary Wong’s Answer
[Gary Wong, 1997.]
Hmm, looks like the first player to roll a 6 gets a tremendous advantage. If he rolls 6-6, he puts 3 opposing checkers on the bar. And if he rolls any other combination with 6, he gets an anchor and 2 opposing checkers on the bar.
I guess 11/36 probability of this happening makes the situation a double/take for whoever is on roll, right? So the cube gets turned every roll until somebody rolls a 6?
In that case, the expected gain of the player on roll (after doubling, ignoring gammons and backgammons), from this roll only, is
| 11 |
| 36 |
The expected gain of the opponent on the turn after is
| 25 |
| 36 |
| 11 |
| 36 |
| 25 |
| 36 |
| 11 |
| 36 |
Thereafter, the expected gains continue increasing at a factor of 2 (for the cube) times 25/36 (for the probability of the game lasting that long),
| 25 |
| 36 |
| 50 |
| 36 |
So the total expected gain is the difference of the odd or the even terms (depending which player you mean) of the geometric series
| 22 |
| 36 |
| 50 |
| 36 |
But since r > 1, the series never converges, and so the expected gain for both players is infinite, right? And so is the expected loss! That sure counts as “extraordinary” in my book!
Color Me Skeptical
[Brian Sheppard, 1997.]
Expected gain is infinite? Not at all! The expected gain in a backgammon game is never more than triple the cube. I don’t know where you made your error, but you can rest assured that there is one.
The way to analyze this type of position is with a “recurrent equation.” In this type of equation the quantity you wish to evaluate comes up as a term on both sides of the equation after you analyze a few rolls. In this case, owing to the symmetry of the position, we obtain a “recurrence” of the quantity after just one roll.
Let’s analyze the cubeless case first. Let x be the equity of the side to move, and let e be the equity of the side to move, given that he rolls a 6. Then we have the following equation:
In 36 rolls, the side to move will have 11 sixes, winning e each time, and 25 misses, in which case he loses x since the situation is exactly reversed. Therefore,
| 11 |
| 61 |
In words: Multiply the value of the position after rolling a 6 by 11/61 to obtain the equity for the side to move.
When we take the cube into account, that changes things slightly. Let y be the equity after the opponent takes. In 36 rolls, the side to move will win e in 11 rolls, and will lose 2y in 25 rolls (because the opponent will redouble). Now the equation is
| 11 |
| 86 |
To sum up: The side to roll should double, to raise his equity from 11⁄61 ⋅ e to 2 ⋅ 11⁄86 ⋅ e. The other side should take because 11⁄61 ⋅ e is definitely less than 1.
Bob Koca Explains
[Bob Koca, 1997.]
Brian’s recursion method normally works, however it depends on the expected values actually existing. Here they don’t. Many people find examples of this sort confusing and I believe some of that stems from not knowing exactly what expected value means.
Not getting overly technical, expected value can be thought of as the long term average. For example let’s look at a very simple case. You have two checkers on the 3 point, opponent has 2 on ace point and the cube is centered.
|
| Black on roll. |
Black wins the game immediately if he rolls two numbers both greater than 2 (16 ways out of 36) or if he rolls double 2’s (1 way out of 36). That’s 17/36 ways to win immediately. If black doesn’t get both checkers off this roll, he loses the game (the other 19/36 times).
Black’s expected gain is:
| 17 |
| 36 |
| 19 |
| 36 |
| −2 |
| 36 |
| −1 |
| 18 |
What this means is that as more and more games are played from this starting position the average gain to the player on roll will eventually get closer and closer to −1/18. (The exact mathematical statement is basically this, but rigorously deals with “eventually” and “gets closer and closer.”)
Suppose we played Paul’s position many, many times. The average winnings will never settle down to a limit. The reason is that there will be eventually huger and huger amounts of points lost on a single game. Enough to knock off whatever progress was made towards the average gain approaching a limit.
As an aside, I’ve seen several posts in the past stating that equities exist for backgammon and describing a recursive method to calculate them. This only works if positions such as Paul’s will never occur.
The concept of undefined expected values is a little tricky and a little counterintuitive. If you are interested in exploring it further I would suggest looking at definitions of expected value, the weak and strong laws of large numbers, and the Cauchy distribution (an example in which expected value does not exist, even though the distribution is symmetric). All of these will probably be in a good undergraduate level probability text.
Some Questions
[Brian Sheppard, 1997.]
Gary, it seems, has grokked the real issue. I can get my head around the concept of “undefined expected values” for only moments at a time, and then it slips away. Perhaps if you could answer a few questions it might help me to understand what is going on.
- Am I correct to say that the situation arises because the payoff
is increasing at a factor of 2 per turn (because of the cube turn) but
the probability of that payoff is decreasing at the rate 25/36 (which
is greater than 1/2)? The point is that the chance of a huge payoff is
decreasing, but the payoffs are increasing faster.
- Suppose we take a sample of outcomes from this game, and
observe the average amount won as time goes on for an indefinite
number of games. Given an arbitrary positive number n, is it true
that the series of averages will eventually be larger than n? Is
it also true that the series of averages will eventually be less
than −n?
- Is it correct to double? If it is not correct to double,
then the position does have a theoretical equity. (But, what is
the basis for deciding when to double if there is no equity to
reason about?)
- Is it correct to take? If it is not correct to take, then
the position does have theoretical equity.
- If doubling and taking is correct, then this position has
undefined equity. That means that positions that lead to this have
undefined equity and so on. What process, if any, prevents backgammon
as a whole from having undefined equity?
- I am curious about computer evaluation of this situation. Does Jellyfish double for the side to roll?
Thanks in advance to anyone who can answer any of these.
Follow-Up
Bob Floyd
As Paul Tanenbaum alluded to in his post, Paul was not the first to discover a position where progressive doubling makes the equity “infinite” (or undefined).
In 1982, Bill Kennedy was trying to create a position that was a perpetual redouble/take (see “Perpetual Redouble?”). When he showed his position to Bob Floyd, Floyd realized the implications of a position that cycles around on itself so quickly. He wrote about undefined equity in his article, “Riding the Tiger.”
Is This Position Legal?
Paul posted his “extraordinary” position to rec.games.backgammon in 1997. But it wasn’t until 2017 that somebody (Nack Ballard) pointed out that this position cannot be reached through legal play.
|
| What position and roll precedes this position? |
But there are many similar positions that can be reached through legal play (such as Bill Kennedy’s) which also have undefined equity.
Adding Up the Pieces
We can try to calculate the equity of this position by adding up the equities of each possible outcome.
For ease of calculation, let’s assume that the player who rolls a 6 first wins a gammon. (Sure, he won’t always win a gammon — he might not even win the game — but most of the time he will, and sometimes he’ll even win a backgammon.)
And we also assume each time that the player to roll will double and his opponent will take.
- If black enters immediately (after double/take), he gets 4 points — 2 for the gammon times 2 for the cube. That happens 11/36 times.
- If black misses and white enters, black loses 8 points — 2 for the gammon times 4 for the cube. That happens 25/36 (for black’s miss) times 11/36.
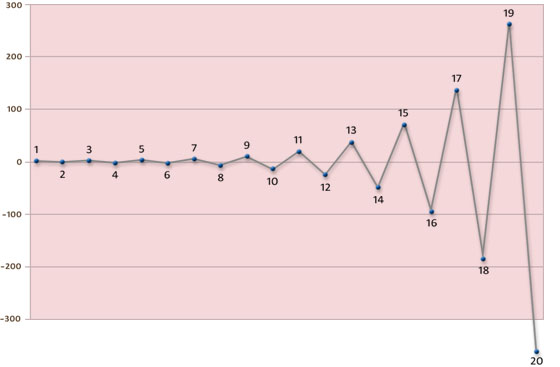
The following table shows the results for the first 20 possibilities.
“Roll” is the first roll that enters a checker from the bar; i.e., the first time a player rolls 6-x.
“Points” is the number of points won or lost from black’s point of view; it is either +2 times cube when black wins a gammon, or −2 times cube when black loses a gammon. The cube doubles every turn.
“Probability” is the likelihood of that situation happening. The first probability is 11/36, because that is the chance of rolling a 6 with either of two dice. On each successive turn, the probability multiplies by 25/36 because that is the chance of a miss on the previous turn.
“Expected W/L” is the expected win or loss. It is “Points” times “Probability” and represents the contribution of this situation to the total equity of the position.
“Sum So Far” is the sum of all the Expected W/L’s so far.
Our hope is that because the probability of each situation goes down each time, the total expected wins and losses will approach some finite value.
| Roll | Winner | Points | Probability | Expected W/L | Sum So Far |
| 1 | Black | 4 | .30556 | 1.22222 | 1.22222 |
| 2 | White | −8 | .21219 | −1.69753 | −0.47531 |
| 3 | Black | 16 | .14736 | 2.35768 | 1.88237 |
| 4 | White | −32 | .10233 | −3.27456 | −1.39218 |
| 5 | Black | 64 | .07106 | 4.54800 | 3.15581 |
| 6 | White | −128 | .04935 | −6.31666 | −3.16085 |
| 7 | Black | 256 | .03427 | 8.77314 | 5.61229 |
| 8 | White | −512 | .02380 | −12.18492 | −6.57263 |
| 9 | Black | 1024 | .01653 | 16.92350 | 10.35087 |
| 10 | White | −2048 | .01148 | −23.50486 | −13.15399 |
| 11 | Black | 4096 | .00797 | 32.64564 | 19.49165 |
| 12 | White | −8192 | .00553 | −45.34117 | −25.84952 |
| 13 | Black | 16384 | .00384 | 62.97385 | 37.12433 |
| 14 | White | −32768 | .00267 | −87.46368 | −50.33935 |
| 15 | Black | 65536 | .00185 | 121.47733 | 71.13798 |
| 16 | White | −131072 | .00129 | −168.71851 | −97.58053 |
| 17 | Black | 262144 | .00089 | 234.33126 | 136.75073 |
| 18 | White | −524288 | .00062 | −325.46009 | −188.70935 |
| 19 | Black | 1048576 | .00043 | 452.02790 | 263.31855 |
| 20 | White | −2097152 | .00030 | −627.81653 | −364.49798 |
| .99932 | −364.49798 |
Unfortunately it doesn’t work. The ever increasing value of the cube makes each new situation count more than the previous one and the expected win or loss gyrates between larger positive and negative values.
The progressing sum of the expected values is shown in the plot below.
The right logic at the wrong time
The situation reminds me of the “proof” that 2 equals 1:
| Let: | a = b |
| Multiply both sides by a: | a2 = ab |
| Add a2 to both sides: | a2 + a2 = a2 + ab |
| Simplify the left side: | 2a2 = a2 + ab |
| Subtract 2ab from both sides: | 2a2 − 2ab = a2 + ab − 2ab |
| Simplify the right side: | 2a2 − 2ab = a2 − ab |
| Factor: | 2(a2 − ab) = 1(a2 − ab) |
| Cancel (a2 − ab) from both sides: | 2 = 1 |
You may wish to ponder this before going on. Can you find the error? (Maybe there is no error!)
Each step looks so simple; how could it be wrong?
It turns out the error is in the final step. “Cancelling” really means dividing both sides by (a2 − ab). But if you look closely and remember that a = b (from Step 1), you see that dividing by (a2 − ab) is actually dividing by zero.
You can divide numbers by a lot of things, but zero is not one of them.
