Money Game Equity Charts?

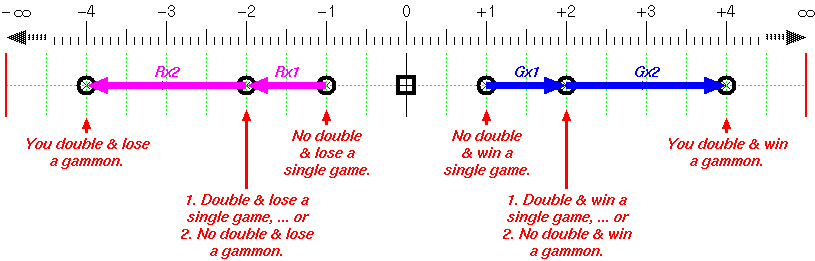
Unlike the one for match plays, a equity chart for money games is quite simple: One dimensional.

Equity chart for money games.

Following explanations are only to show how gain-risk arrows differ from those for match plays. In order to make the comparison simple, I ignore doubled player's re-cube effect and any backgammon wins and losses. I also assume that a gammon win is still possible for both players.

Gain-Risk ratio in a "Double/No-double" decision

Double to 2 in a money games

	No double & win a single: You only get 1 point.	Gain = 1 (= 2 - 1)
	Double & win a single: You get 2 points.
	No double & win a gammon: You only get 2 points.	Gain = 2 (= 4 - 2)
	Double & win a gammon: You get 4 points.
	No double & lose a single: You only lose 1 point.	Risk = 1 (= 2 - 1)
	Double & lose a single: You lose 2 points.
	No double & lose a gammon: You only lose 2 points.	Risk = 2 (= 4 - 2)
	Double & lose a gammon: You lose 4 points.

Main characteristics of those arrows are fairly simple. Ratio between gain and risk is always 1:1. Gx2 and Rx2 are twice as long as Gx1 and Rx2.

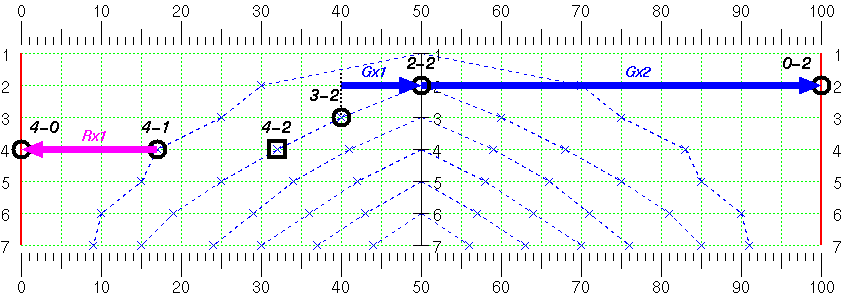
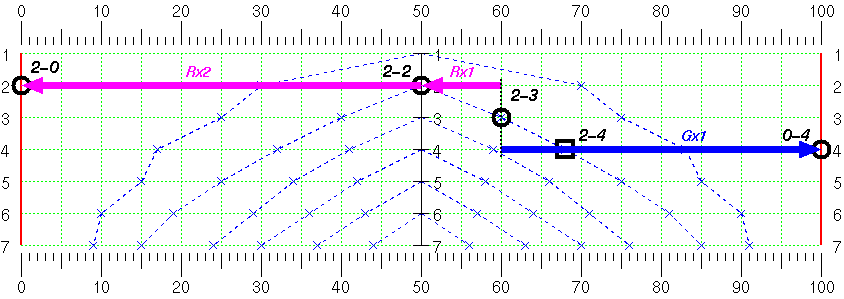
Compare ratio of "Gx1", "Gx2", "Rx1", and "Rx2" arrows in the chart above with ones for a doubling decision in a match at 4away-2away score below.

Double to 2 in a match at 4away-2away

First of all, "Rx2" no longer exist, because losing a gammon with 2 cube has no difference from losing a single game with 2 cube.

Secondly, the ratio Gx2:Gx1 in this score is much bigger than in money games. It's always 2:1 ratio in money games, but in this score the ratio jumps up to 5:1. That means doubling at this score is more effective when you have some chance to gammon your opponent than in money games.

One more thing to note is that Gx1 is much shorter than Rx1. That implies that you are less inclined to send the cube when you don't have any gammon chance at all than in money game.

Gain-Risk ratio on a "Take/Pass" decision

Well known "25%" theory applies here. Ratio of Rx1 to Gx1 is 1:3, or Rx1 is 25% of total of risk and gain 4 (=1+3).

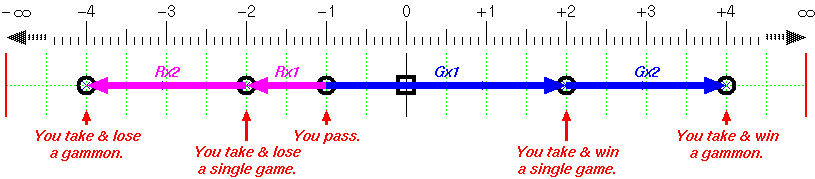
Compare that with a take/pass decision in a match play at 2away-4away score below.

Take/pass decision for 2 cube in a match at 2away-4away

The ratio of Rx1 to Gx1 is somewhat smaller (1:4), suggesting that you may take this 2 cube more aggressively than in money games only if your gammon loss chance is small enough.

You don't have Gx2 now, that means that your gammon win has no extra value to a single win if you take this cube.

On the other hand, the ratio Rx2 to Rx1 is now 5:1 as oppose to 2:1 in money games. That implies you must be more conservative on this take when a chance of your gammon loss is there.