|
| Cube Theory |
 In recent issues of your magazine there have been several articles and letters concerning the option of "beavering" a double. The question is whether or not the beavering option would ever be used by skillful players (i.e., players who do not make foolish mistakes).
In recent issues of your magazine there have been several articles and letters concerning the option of "beavering" a double. The question is whether or not the beavering option would ever be used by skillful players (i.e., players who do not make foolish mistakes).
Many people seem to think that it can never make sense to offer or accept a beaver. Their reasoning goes like this: a player will not beaver a double unless his/her expected value of the game is positive, in which case the other player would not have doubled. Other people claim (often with flimsy or faulty evidence) that there are positions where the correct play is to double and then beaver.
The fact is that in a sense both sides are correct. The confusion stems from the "Jacoby doubling rule," which states that a gammon does not count as double stakes unless the cube has been used.
Without the Jacoby rule, the first claim is correct since an accepted double merely doubles both player's expected value of the game.
With the Jacoby rule, the first double actually changes the scoring rules. An accepted double does not exactly double both players expected values, and it turns out (at least theoretically) there are positions where a beaver is the logical outcome. With the Jacoby rule, a player with a negative expected value may want to double, hoping to win extra for a gammon. In many cases, the expected value will become less negative, or perhaps even positive, so the player should consider doubling. If the expected value is still negative after a double, the opponent should beaver. The following example illustrates the point.
|
| White on roll. |
| E1(W) = 2(11/36) − (25/36) = −3/36. |
If White doubles and Black accepts but does not beaver, the expected value is:
| E2(W) = −6/36. |
Clearly, Black would beaver a double, so
| EB(W) = −12/36. |
Obviously, White will not double.
On the other hand, if the game is being played with the Jacoby rule, then:
|
E1(W) = 11/36 − 25/36 = −14/36, E2(W) = 4(11/36) − 2(25/36) = −6/36, EB(W) = 8(11/36) − 4(25/36) = −12/36. |
Thus, White doubles and Black beavers.
Some simple algebra shows what's going on. Consider an arbitrary position in which (for simplicity) the probability that White will be gammoned is negligible. Let
| PG(W) | = probability that White gammons Black, |
| P1(W) | = probability that White wins (no gammon), |
| P1(B) | = 1 − PG(W) − P1(W) = probability that Black wins. |
Thus,
| E1(W) | = PG(W) + P1(W) − P1(B), |
| E2(W) | = 4PG(W) + 2P1(B), |
| EB(W) | = 8PG(W) + 4P1(W) − 4P1(B). |
- If E2(W) > E1(W) and EB(W) > E1(W) (i.e., if 4PG(W) + 2P2(W) > 1), then White will double.
- If E2(W) > 1 (i.e., if 6PG(W) + 4P1(W) < 3), then Black will accept a White double.
- If E2(W) < 0 (i.e., if 6PG(W) + 4P1(W) < 2), then Black will beaver a White double.
The following graph shows the correct decisions as functions of PG(W) and P1(W).
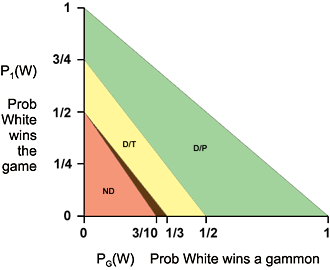
|
|
The Jacoby rule is not a standard backgammon rule. Thus, in tournaments and in private games where the Jacoby rule is not being used, there can never be a position where a player would be tempted to beaver a double unless the double was a serious blunder. If the Jacoby rule is in effect though, positions in which a beaver is the logical outcome may occur surprisingly often.
about this position.