Sometimes one wants to strip away the luck. Is move A better than move B? Is player X stronger than player Y? A proper respect for the luck in the game is needed. Below, we will consider a method for cancelling most of the luck in backgammon, and will apply it to analyze a game between the computer programs Jellyfish and Snowie, both set on levels much stronger than I am.

I call the following equation the fundamental equation of games of luck and skill:

Final  −  Initial  =  Net Luck  +  Net Skill

Final refers to the final score. This might be +1 or −4 for a money game, or 100% mwc (match winning chances) or 0% mwc for a match. Initial refers to the starting equity or mwc of the situation considered. Net Luck  as outlined in "A Measure of Luck," has average value 0 on each roll. It also has average value 0 in each game or match. Net Skill is the difference in the total magnitude of the errors of the players when compared with technically perfect play.

When rolling out a position (comparing play A with play B), we start with a position (or two) whose equity we do not know. We might have Jellyfish play both sides many times, so we hope that the Net Skill is 0, that Jellyfish makes errors of equal magnitude from both sides of a position. This may be unreasonable if one side's choices are easy and the other side's are difficult, and must be reassessed with each rollout. Let us rearrange the fundamental equation under the assumption that Net Skill is 0:  Initial = Final − Net Luck.

After rolling a position out, the final result is clear, but what we want is different by the Net Luck. Over a long rollout, the average Net Luck will be close to 0, but we can do better than that. One way is to compute an Estimated Net Luck fairly, and subtract that from the result of the rollout. The estimate Initial ~ Final − Estimated Net Luck will be off by the difference between the actual Net Luck and the Estimated Net Luck, and with an accurate, unbiased estimate of luck, we will get an accurate, unbiased estimate of the equity of the position.

Suppose two excellent players play. To find the Net Skill displayed, we could use Snowie to estimate the errors made by each side. Unfortunately, that method is biased. Suppose one of the players is Snowie: Snowie does not play perfectly, but it would rate its own play as perfect, and would reward those whose play resembles Snowie's rather than perfect play. Instead, let us consider the fundamental equation applied to a game. The initial position is even (we don't know who will win the first roll) so the Initial equity is 0. Thus, we can rewrite the equation as Net Skill = Final − Net Luck.

The final result of a rollout is a fair estimate for the initial equity, but often not a good enough estimate. It would completely ignore the effect of luck, and would be incorrect by the average Net Luck. The idea of variance reduction is to compute an Estimated Net Luck fairly, and subtract that from the final result instead. This is off by the average amount of the Net Luck − Estimated Net Luck.

Snowie estimates the luck in a roll by estimating the equity of the best play it sees after rolling, and subtracting the equity of the position before rolling. This is a good estimate, and is equivalent to measuring skill by summing up the errors compared with what Snowie thinks is the best play. I have found this to be tremendously helpful, but because Snowie does not estimate the equity perfectly, this method is biased, and unsuitable for analyzing matches between players close to Snowie's level or in positions where Snowie is less reliable. However, one can fix any estimate of match winning chances to produce an unbiased estimate. An evaluation as good as Snowie's may be corrected to eliminate most of the luck in backgammon without bias.

Instead of comparing the evaluation of the apparently best play after rolling with the estimated equity before rolling, just ask whether the roll was above average or below average. This ensures that the estimated luck will average to 0. Example: Suppose Snowie currently evaluates a position as worth 0.2, but precisely half of the rolls would leave a position Snowie believes is worth 1 and half of the rolls would leave a position Snowie believes is worth −1. Snowie's estimate of the luck if one rolls well is +0.8. Since the average is 0, the unbiased estimate should be that the luck is +1. To be fair, one must evaluate the initial position one ply deeper than the position after rolling.

All of the evaluations are in the unusual units of match equity, which is +1 for a won match and −1 for a lost one. The perspective is always that of Jellyfish, so a bad roll for Snowie shows up as positive luck. Note that the evaluation for a given move does not always agree with the average for the next move, even when these correspond to the same position. Average is the higher ply evaluation.

	Jellyfish	Snowie
1	5-2:  13/8, 24/22 Average/Evaluation/Luck: 0.000 / 0.012 / +.012	6-3:  24/15 A/E/L: 0.010 / 0.057 / +.047
2	3-3:  13/10*(2), 8/5(2) A/E/L: 0.054 / 0.284 / +.230	2-3:  B/22, 24/22 A/E/L: 0.283 / 0.261 / −.022
3	4-2:  24/20, 22/20 A/E/L: 0.255 / 0.266 / +.011	2-1:  6/3 A/E/L: 0.265 / 0.307 / +.042
4	3-2:  13/10, 13/11 A/E/L: 0.308 / 0.257 / −.051	4-2:  8/4, 6/4 A/E/L: 0.256 / 0.289 / +.033
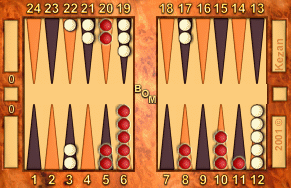
5	3-2:

Red to play 3-2 R: 137, W: 154

	Jellyfish	Snowie
5	3-2:  11/8, 6/4 SW Tiny, 20% and SW 1-ply prefer 11/8 10/8, but SW Huge, 100% agrees with this play. A/E/L: 0.282 / 0.238 / −.044	5-4:  13/8, 13/9 A/E/L: 0.226 / 0.307 / +.081
6	3-1:  10/7, 8/7 A/E/L: 0.307 / 0.261 / &minus.046	6-3:  13/10, 9/3 0.250 / 0.343 / +.093
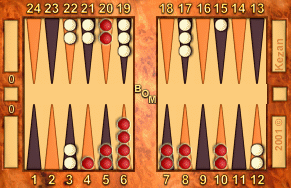
7	4-1:

Red to play 4-1 R: 128, W: 136

	Jellyfish	Snowie
7	4-1:  20/15* Holding the anchor with 8/4 8/7 is preferred by SW Huge, 100% (by 0.1% mwc) and by Tiny, 20%, though 1-ply rates them as equal. A/E/L: 0.362 / 0.238 / −.124	1-2:  B/23, 22/21* A/E/L: 0.232 / 0.137 / &minus.095
8	4-1:  B/20 A/E/L: 0.161 / 0.284 / +.123	5-4:  21/12 A/E/L: 0.277 / 0.386 / +.109
9	1-1:  15/13*, 10/9(2) A/E/L: 0.391 / 0.510 / +.119	3-2:  B/22, 23/21 A/E/L: 0.491 / 0.448 / −.043
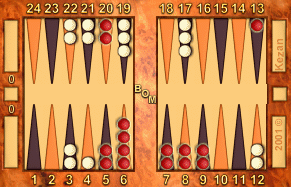
10	2-1:

Red to play 2-1 R: 135, W: 147

	Jellyfish	Snowie
10	2-1:  13/11, 6/5 SW Huge, 100% prefers 6/4* 6/5 by 0.06% mwc, though Tiny, 20% agrees with not hitting. 1-ply rates them as equal. A/E/L: 0.455 / 0.464 / +.009	6-3:  21/12 A/E/L: 0.458 / 0.420 / −.038
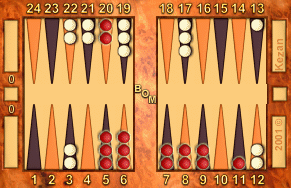
11	4-2:

Red to play 4-2 R: 132, W: 138

	Jellyfish	Snowie
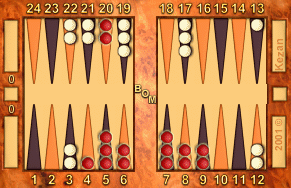
11	4-2:  11/7, 6/4 All Snowie levels preferred 11/5, Huge, 100% by 0.20% mwc. A/E/L: 0.414 / 0.374 / −.040	1-4:

White to play 1-4 R: 126, W: 138

	Jellyfish	Snowie
11		1-4:  22/21*, 8/4 SW Huge, 100% prefers 22/21* 12/8 by 0.17% mwc A/E/L: 0.351 / 0.181 / &minus.170
12	3-2:  B/20 A/E/L: 0.231 / 0.266 / +.035	3-2:  13/10, 12/10 A/E/L: 0.300 / 0.374 / +.074
13	4-2:  7/3*, 5/3 A/E/L: 0.409 / 0.294 / −.115	5-4:  B/21, 13/8 A/E/L: 0.271 / 0.047 / −.224
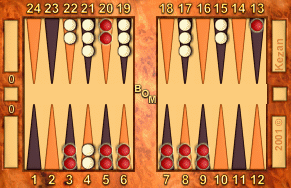
14	5-2:  20/13 A/E/L: 0.077 / 0.117 / +.040	5-5:

White to play 5-5 R: 129, W: 122

	Jellyfish	Snowie
14		5-5:  8/3(3), 6/1 Snowie flings the dice across the room. This worst possible roll is almost a full point behind 6-6. A/E/L: 0.112 / 0.303 / +.191
15	3-4:  13/6 A/E/L: 0.314 / 0.316 / +.002	3-1:  4/1, 3/2 A/E/L: 0.310 / 0.219 / −.091
16	5-4:  20/11 A/E/L: 0.227 / 0.181 / −.046	4-1:  6/2, 6/5* A/E/L: 0.193 / 0.228 / +.035
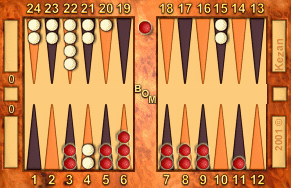
17	5-5:

Red to play 5-5 R: 118, W: 93

	Jellyfish	Snowie
17	5-5:  B/20*, 11/1, 6/1 All levels of Snowie prefer B/20* 11/6 7/2(2), Huge, 100% by 0.62% mwc. A/E/L: 0.284 / 0.618 / +.334	2-2:  B/21, 10/8(2) A/E/L: 0.590 / 0.468 / −.122
18	5-3:  20/12 A/E/L: 0.526 / 0.517 / −.009	1-2:  8/5 A/E/L: 0.499 / 0.546 / +.047
19	6-5:  12/1 A/E/L: 0.626 / 0.593 / −.033	3-4:  8/1 A/E/L: 0.607 / 0.654 / +.047
20	5-3:  8/3, 8/5 A/E/L: 0.702 / 0.654 / −.048	3-1:  5/2, 3/2 A/E/L: 0.686 / 0.763 / +.077
21	6-1:  7/6, 7/1 A/E/L: 0.761 / 0.695 / −.066	3-3:  21/9 A/E/L: 0.707 / 0.634 / +.073
22	3-2:  6/1 A/E/L: 0.634 / 0.563 / −.071	5-2:  9/4, 3/1 A/E/L: 0.548 / 0.589 / +.041
23	5-1:  6/5, 6/1 A/E/L: 0.589 / 0.499 / −.090	6-3:  21/12 A/E/L: 0.432 / 0.386 / +.046
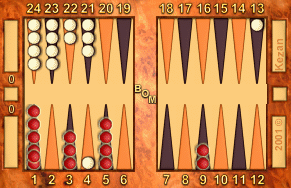
24	6-6:

Red to play 6-6 R: 53, W: 63

	Jellyfish	Snowie
24	6-6:  9/3(2), 5/O(2) A/E/L: 0.451 / 0.932 / +.481	3-4:  12/5 A/E/L: 0.909 / 0.929 / +.020
25	6-6:  5/O(2), 3/O(2) A/E/L: 0.910 / 0.991 / +.081	1-2:  21/19, 2/1 A/E/L: 0.994 / 0.995 / +.001
26	4-3:  3/O(2) A/E/L: 0.998 / 0.997 / −0.001	5-5:  19/4 5/O A/E/L: 0.998 / 1 / +.002
27	3-3:  3/O 1/O(3) A/E/L: 1 / 1 / 0	1-2:  3/O A/E/L: 1 / 1 / 0
28	1-5:  1/O(2) A/E/L: 1 / 1 / 0	3-3:  4/1(3) 3/O A/E/L: 1 / 1 / 0
29	4-5:  1/O A/E/L: 1 / 1 / 0

The total estimated luck for Jellyfish is +0.865. The outcome was +1, so the estimated net skill was that Jellyfish was stronger by +0.135, or 6.8% mwc.

Is this accurate? No, but it is much closer than saying that Jellyfish will win all the games since it won the first one. We performed variance reduction, not variance elimination. This result is probably further from the correct value than would be obtained by using the biased analysis of Snowie directly. There is still some noise on top of the signal, but it will take a much shorter sequence of matches for this noise to be essentially 0 than if one were not to try to cancel out the luck. My guess is that there is a factor of 1/5 to 1/10 as much noise as before, and that this would be reduced much more by using 2-ply or 3-ply evaluations.

One should keep in mind that the level of skill is also subject to change, since the player might be better or worse at handling blitzes, backgames, or holding games. This may be viewed as another source of noise that is not affected by the variance reduction. Even within a type of game, a player might make more or fewer errors at random. So even with a perfect estimate of the Net Luck, one would need a few games of each type to estimate the average skill displayed.

If the example match above were hedged, then Jellyfish would collect 0.135 times the stakes from Snowie: 1 for winning − 0.865 in side bets.

An odd effect of hedging would be that one would probably owe something after winning a short blitz—it is hard to blitz correctly, and easy to be blitzed correctly, so one's luck while blitzing usually exceeds the point won. Would it be worthwhile to avoid positions like this which are hard to play? As with regular backgammon, yes, but only if avoiding the hard position is less of an error than one expects to make while playing it.

What difference does it make if the bot whose evaluations are used is stronger? The quality of the estimate of Net Skill is beneficial but not very important as long as it is unbiased. Bots which play better will tend to have better estimates, which means that there will be less noise added to the payoffs. If one plays through positions that the evaluator does not understand well, there may be larger variations. These sources will be added to the natural variations in the actual displayed skill. Reducing the noise from the estimate a few percent by using rollouts would be like adding more insulation to the walls without closing the window. For intermediate players and above, though, the error in the estimate of Net Skill is nowhere near the oscillations from the unhedged luck of the dice.

Suppose I play 25 1-point matches with a bot stronger than I am by 10% mwc, i.e., it will win 3 out of 5 matches. It should win 15 of the 25 matches, but due to variations in luck, 15% of the time it will win at most 12, and 15% of the time it will win 18 or more matches. There is almost a 1/3 chance that the estimated skill difference would be off by more than 12%. By the FIBS ratings formula, rather than being ahead 350 rating points the bot might appear to be 825 points ahead or 65 points behind.

What happens if we hedge the matches? That depends on a few things. I believe the following are plausible assumptions:

Suppose our Net Skill varies by +−10%, that is, half the time we play equally well, and half of the time I throw away 20% more equity than the bot. Suppose the bot's estimate is off by +−10% each time. Then 88% of the time the adjusted score would be as though the bot won between 14 and 16 matches, between 215 rating points and 505 point ahead, and over 99% of the time the hedged score would be as though the bot won between 13 and 17 matches. To achieve the same level of accuracy without hedging, we would need to play more than 10 times as many matches.

Much as I have enjoyed playing hundreds of matches and money games against Jellyfish and Snowie to see if I learned anything from reading a backgammon book, variance reduction of skill is the feature I would most like to see in the next editions of backgammon programs.