Book Transcription

Foreword

It must not be regarded as egotistical to attempt authorship of a book on backgammon. The historical and more recent material required are matters which have entailed only the most casual research and even more casual experience. The mathematics involved are more elementary than advanced, and it is one of the charms of the game that they are practically of minor importance.

So far as comments or observations are concerned, little is possible beyond the comprehension of a child of ordinary intelligence and little is possible of expression beyond quite immature powers of composition.

For backgammon even in its modern development is not an appropriate subject for serious study. It is primarily a pleasant pastime requiring no greater mental effort than that of alertness. While we may, and very generally do, cherish with our other illusions ideas of superior skill and understanding, in the realm of backgammon the goddess of chance generally reigns supreme.

If we are alert and avoid obvious blunders, and sometimes when we do neither of these things, it is generally the throw of the dice that determines the result. It is what those who have lost hope — and the game — regard as blind chance and refer to cynically in terms of opprobrium; while their complacent opponents, chortling with self-satisfaction, entertain ideas of demonstrated mental superiority.

Let us not so deceive ourselves. Backgammon always resolves itself into a game of dice. We, the experienced, with the humility of that bitter school, must realize that of far greater importance to the result of a game than the intelligent, and tedious, deliberation of the player is the most casual smile of the divinity referred to.

To write of backgammon, beyond its origin, which is lost in antiquity, its history, of which little is known, its description, which is simple, and its rules, which are few and unimportant, one should really write of luck, good and bad, and the smiles and frowns of fortune. Unfortunately of such a subject nothing is known. It is not merely difficult like the fourth dimension, relativity or non-Euclidean geometry. It is impossible — beyond the impenetrable veil and eternally obscure.

Upon such a subject either a child of ordinary intelligence or the greatest savant could write with equal understanding and authority. Accordingly, when in the nature of things to be qualified is impossible, it is not precisely egomania to feel comparatively so.

Having indicated by the foregoing paragraphs how impossible it is to say anything intelligent or even intelligible upon what is the true subject of this book, we shall nevertheless proceed. And we may add that we do this with no great forebodings, for observation has led us to believe that popular interest has little relation to the qualifications of writers and conversationalists. The treatises of the erudite are no more popular than the lectures of the learned, while the most absorbing “best sellers” and most delightful conversations seem frequently to emanate from brains untroubled by knowledge of any kind, least of all the subjects selected.

By confessing at the outset, not guilt, but innocence of any real knowledge of this game, We trust that we are avoiding for this book the position of an authority, with the unpleasant responsibility and limited circulation which would be then inevitable. We prefer rather that it should be regarded as quite unauthoritative, irresponsible, even frivolous if necessary, so that it may be as popular as backgammon in its modern development is so rapidly becoming, among the alert if not among the serious-minded.

Grosvenor Nicholas.
New York,
January 4, 1928.

Chapter I

Past And Present

While the name backgammon, by which we know this game, is from the Saxon,¹ the game itself is of much more ancient origin. It was probably known in ancient Egypt and surely in Ur of the Chaldees more than 5,000 years ago. This appears from the recent report of the director of the Mesopotamian expedition of the University of Pennsylvania and the British Museum, which contains the following:

“The gaming board found in the King’s grave is not so richly decorated as one found last season in Ur, but is made more interesting by the fact that beneath it were found in neat piles the two sets of playing pieces and the dice. One set of ‘men’ is composed of simple black squares inlaid with five dots each, and the other is of shell squares engraved with animal scenes. One set of dice is shell with lapis dots; the other of lapis with gold dots.”

Plato alludes to the same or a similar game, which was known to the ancient Greeks, and the Romans also played ludus duo decim, the “twelve line game,” which must have been in fact backgammon or something very similar.

Moreover, dice and dice boxes were already almost literally as old as the hills. They were in common use in Greece, Rome and the Orient in most ancient times. They are mentioned as an Indian game in the Rig-Veda and in Egypt are found in the tombs of the kings. Herodotus attributed dice to the Lydians, while Sophocles ascribed the invention of dice to Palamedes, who used them for the entertainment of his compatriots during the siege of Troy.

It is interesting to note that the ancient Greeks, with whom dice were very popular, expressed their emotional reactions at good and bad throws in much the same fashion as do many of our backgammon players of to-day. They called sixes, which were high, “Aphrodite,” and aces, which were low, “dog,” or its Greek equivalent.

In the Roman empire dice went as big as the Colosseum or Circus Maximus and dicing must have been regarded as “the sport of kings,” or one of them. One of the emperors set apart a special room in his palace for dicing and the Emperor Claudius wrote a book on the subject. The Emperor Domitian was an adept and Caligula a cheat. It is familiar history that Antony risked an empire by remaining in Egypt, but the reader probably does not know that he also took a chance with Cleopatra at throwing dice. We do not know this either, but we believe it, for in that immortal liaison there must have been “meanwhiles” in a sense other than Mr. Wells has given that word.

The antiquary Thomas Hyde, in his Syntagma, records his opinion that the game “odds or even,” played with pebbles, is nearly coeval with the creation of man. How many eons passed before our progenitors developed intelligence sufficient to transmute the pebbles into dice we do not know. The invention may have been contemporaneous with the invention of the canoe, the wheel, or of wine-making and socially of secondary importance no doubt only to the last.

In like manner we do not know the beginning of backgammon. Who it was who first conceived the idea of a table and elaborating the game of dice by moving pieces according to the throws, history does not record. However, these early developments, the Roman “twelve line game,” Chaucer’s “Tables” or backgammon as it has been since known in England and “tric-trac,”² as it has been known upon the Continent, appear to have been insufficient. Notwithstanding them, since the Middle Ages dicing apparently declined, supplanted more and more by card playing and other more elaborate forms of gaming.

It has remained for the Twentieth Century to further elaborate the game of backgammon, by the introduction of “doubling” and “chouette” and give us modern backgammon. This new game is gaining ground so rapidly that the sun seems destined again to shine upon dicing as it did in the time of the Caesars. Present circumstances are so propitious that we need consult no Cumean Sibyl or other augury to predict for modern backgammon an unprecedented popularity.

We have first the circumstance that, while the old game of whist achieved a tremendous vogue through its elaboration into “Bridge” and “Auction,” it has now been further elaborated into “Contract” and we have accordingly this unfortunate situation. While “Auction,” like “Bridge,” has passed into the discard, and will naturally be regarded as passé or dead from the standpoint of good society, it is a question to what extent good society will have the patience to familiarize itself with the more complicated elaborations of “Contract.” And it is a question to what extent even the masters of this new game will find it pleasure without alloy to play with the casual exponents, whom they meet in good society, with their casual familiarity with conventions and disastrous consequences almost inevitable.

But the most important circumstance favoring modern backgammon is undoubtedly the present tendency of the times. It has been said that there is a destiny which shapes our ends. Probably this is true, but to-day a paramount force in that destiny is youth and the will to remain young. Formerly this would have had some relation to youth in actual years and it might have meant sweetness, modesty, respect and an exaggerated, and possibly inappropriate, deference to age. To-day it means none of these things. It means energy, restlessness and pleasant or profitable action, rather than tedious or profitless thought or decorum. In short, life as we all wish to live it.

Possibly this implies a sort of hedonistic recklessness and is too severe a commentary upon us. However, is it not true that we are now all so much interested in this conception of youth, so much desire that fountain for which Ponce de Leon sought in vain, that, regardless of years, we find ourselves following the poets’ formula and thinking of all the foolish youthful things we ever did so that we may repeat them and become rejuvenated or, at least, feel so?

That the interest in this modern conception of youth is tremendous and general seems to be beyond question and it is essentially a modern conception. Formerly, within the memory of many of us, there were old gentlemen and grandmothers. These may exist to-day. We presume that the latter must but, excepting among a certain reactionary and diminishing class, known as old-fashioned people, who would ever be aware of it? In spite of the mere passage of time, youth, no longer a matter of years, remains and grandparentage, if it be a scientific fact, exists no more for us than the indestructibility of matter and other facts, known to science, but of which we are quite unconscious and can hardly comprehend.

In the diminishing class to which we have referred, there may also still remain a few old gentlemen. Some of these reminders of bygone days seem to be still preserved in certain city clubs where one may sometimes catch a glimpse of them seated in the windows, smoking cigars, appropriately matured, and looking out upon the Avenue in the best traditional fashion. There may also still remain some of these who sit in easy chairs, gossip with neighbors and watch the young at play. However, fortunately we rarely encounter them.

Formerly the elders enjoyed respect while only the young enjoyed life. Now, we all enjoy life and youthful activities. And if there are still certain old gentlemen, and there may be some of these quite young in years, who hold up their hands in protest against the present loss in respect, they should realize that the change is not without its compensating gain. Instead of becoming mere spectators, we now continue to be participants; and if this means a transformation of our city clubs from grandstands or showcases into emporiums of indoor youthful activities, a development of country clubs for outdoor youthful activities and the preservation of our youth and youthful interest in play, we should not bewail the change.

In the modern ideal of life there are no old gentlemen and there are no old ladies. We all retain our youth and we accomplish this by retaining our interest in youthful activities, games of all kinds and the more youthful the better.

Before coming to our description of modern backgammon, it is difficult to make it clear to the reader how singularly appropriate that game is to this modern conception of youth. However, it is this appropriateness which seems not only to explain, but to insure, the ever growing popularity of the game. The young in years take to it naturally while the balance of our population, old only as a scientific fact, recognize immediately its rejuvenating possibilities. Talleyrand recommended whist to prevent old age becoming dull. In his time old age existed socially as well as scientifically. Had he lived to-day, he would have recommended backgammon as the panacea against being relegated at all to that old-fashioned class, now so nearly extinct.

Following our description of the game, we shall return to this subject. Suffice it here to mention in conclusion that there seems to be at present a very real relation between this modern tendency for youthful activity and backgammon as a panacea. However desirable socially, youthful activity for those of advanced years is not always without its dangers. Heart afflictions have become a graver menace than tuberculosis and are to-day our chief mortal foe. It is fortunate, therefore, that some of this activity is being absorbed by backgammon instead of other more violent forms of amusement.

In fact it will not surprise us if observant physicians, realizing present conditions, take to prescribing backgammon. Should they do this they can point to the longevity of one of our leading backgammon players who, although twenty years past his allotted threescore and ten, has preserved his youthful interest generally and particularly in backgammon. The game, we hope, will preserve him for us many years to come.

Chapter II

The Ancient Game

Backgammon is played by two persons upon a special board with draughtsmen and dice.

The board is divided into four “tables,” each being marked with six “points” colored alternately in two colors. The inner and outer tables are separated from each other by a raised bar and the whole board is surrounded by raised sides.

The board is furnished with fifteen white men for one player and fifteen black men for the other player. These are arranged upon the board as in the following diagram.

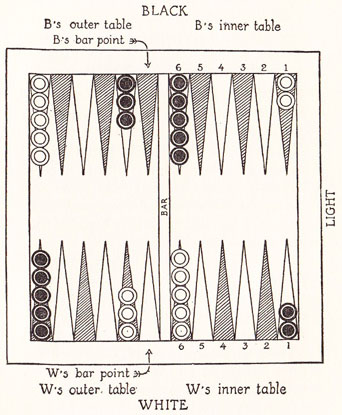
It is customary to arrange the men so that the home or inner tables of the board are nearest the light; and we may say at once, to make our description more intelligible, that the object of each player is to move his men into his inner table and then remove them from the board, both the moving and removing being done according to throws of the dice.

Two dice-boxes are required, one for each player. It is correct to have one pair of dice, which are used by both players, but generally each player is provided with a pair of dice and this is perhaps more convenient.

To determine the right to throw first each player throws one die and the one who throws the higher number adopts both of the numbers thrown as his throw and makes his opening play accordingly. Sometimes the player throwing the higher number is permitted to either adopt the numbers thrown or throw again, using both dice. This seems unwise, as the first play is generally an advantage, and it can hardly improve the game to allow the further advantage of a second throw which may be doublets.

The men are moved on from point to point, according to the throws of the dice made by each player alternately. White moves from black’s inner table to black’s outer table, then across to white’s outer table and thence into white’s inner table. Black moves in the same manner but in the contrary direction into black’s inner table.

A player may move any of his men the number of points corresponding to the numbers thrown by him, provided the point to which the move would bring him is not blocked by two or more of his adversary’s men being upon it. The whole throw may be made with one man, or two men may be moved, one according to one of the die thrown and the other according to the other die. If doublets are thrown, four moves of the numbers thrown may be made either all by one man or separately.

For example, if white throws a six and five, he may move one of his men from black’s inner table six points to black’s outer table and thence five points farther on, placing the same upon the point with the five white men already there. If white throws double fives, he cannot move either of his men from black’s inner table, for a move of these men five points is blocked by the opponent’s five men upon the six point of black’s inner table. In the event of such a throw, white might move two of his men from black’s outer table each five points to his own outer table, and thence five points farther on to his inner table, when his play would be complete.

Any throw or part of a throw which cannot be played is of no effect. However, it is compulsory for a player to move the whole throw if possible and, if he can play either one, but not both, of the two numbers thrown, he must play the larger.

When a player moves so as to place two or more men on the same point, he is said to “make a point.”

A single man upon any point is called a “blot.” When a player throws a number which enables him to place a man upon a point occupied by a blot, the blot is said to be “hit” or “taken up.” The man so hit is taken up and placed upon the bar separating the inner and outer tables. He must then begin again by entering the adversary’s inner or home table, which he may do upon his next throw, provided it results in a number that corresponds to the number of an unblocked point.

For the purpose of reentering a man which has been taken up, the points in the home tables are numbered from one to six, from the side of the board to the bar. If the five and three points are unblocked and the throw is five and three, the man upon the bar may be entered upon the five point and a move made of the three, or he may be entered upon the three point, and a move made of the five.

It is generally an advantage to take up blots, because the men taken up must reenter and start anew. A player is not allowed to move any other man while he has one or more upon the bar to enter. It is, therefore, an advantage to make the points in one’s own home table, so that the adversary, if one of his men is taken up, cannot enter. One can then continue throwing and progress while the adversary is unable to move.

The game proceeds until one of the players has moved all of his men into his inner or home table. He then proceeds to take his men off the board, that is, to remove them from the points which correspond to the numbers which he throws. If a number is thrown and the corresponding point is unoccupied, a move must be made, if there is room for it, and a move may always be made if desired, instead of removing a man.

In this removing or throwing oil, if the six point is empty, and six is thrown, a man may be removed from the five point or next point occupied and so on. If, after a player has commenced throwing off his men, he: should be hit on a blot, he must enter his adversary’s inner table and move the man into his own inner table again before he can continue throwing off.

The player who is first in removing all his men wins the game.

It is a single game if his adversary has begun taking off his men. If his adversary has not taken off a single man, it is a gammon, or double game and counts double. If he has not taken off a single man and has one or more men in the winner’s inner table or upon the bar, it is a backgammon or triple game.

The object in counting gammons and. backgammons as double and triple games is. to enable the player to increase substantially his score by winning a more decisive victory. This stimulates the interest, encouraging a player to more aggressive and hazardous play whenever there is a reasonable opportunity of thereby achieving a double or triple game.

Another and perhaps better method of creating the same stimulating effect is to play for “points.” In this game, as it is played in New York, there are no double or triple games. The winner scores one point for every man of his opponent remaining in the opponent’s inner table, two points for every man remaining in the opponent’s outer table, three points for every man remaining in the winner’s outer table and four points for every man remaining in the winner’s inner table or upon the bar.

Some people refer to this game as scientific, implying presumably an accurate and systematic knowledge. In backgammon we do not believe such a thing to be possible and rejoice accordingly. While blissfully innocent of any accurate knowledge of the game, it would indeed be folly to be wise.

However, it is true that in the point game the method of scoring is more scientific. The score always accurately represents the result of each game. In a close game the amount scored may be only one or two points, While in an overwhelming victory the points scored may amount to thirty or forty.

In Philadelphia, a somewhat different method of scoring is used. The winner scores one point for every man of his opponent remaining on the board. If the game has resulted in a gammon, that is, if the opponent has not removed a single man, the fifteen points for the fifteen men remaining are doubled, making the game count thirty. In like manner, if it is a backgammon, the points are tripled, making the game count forty-five.

The Philadelphia method seems to make for a larger score and to give a greater incentive for attempting gammons and backgammons. On the other hand, points scored according to the New York method correspond more accurately with the results achieved.

Russian backgammon, a somewhat different game, is played by entering the men in the same table by throws of the dice, instead of setting them up as in the diagram. Both players then move in the same direction. There are several different ways of playing, but as this game has no relation to modern developments, and is not generally played, we shall satisfy ourselves with this brief mention of it.

It must be of interest to players of this ancient game to realize that, had they been kings of Babylon, or of some other remote civilization, or kings of England or of France in the Middle Ages, or even Roman Emperors, they might have been doing the same thing. However, to-day the importance of this ancient game is that it is the foundation of modern backgammon, which we shall describe in the next chapter.

Chapter III

The Modern Game

This is the ancient game plus the Twentieth Century elaborations “doubling” and “chouette.” The former of these additions is just what has been needed to make the game most interesting, sometimes even exciting. The latter has made the game more¹ interesting still and at the same time has overcome the limitations of a two-handed game, transforming backgammon into a game which may be played by any number.

It is said that the doubling, which has so greatly increased the possibilities of the game, as well as its popularity, was first originated on the continent of Europe in connection with the game of golf. It may be described as follows.

After the game has commenced either player may, at any time before he throws his dice, double the stake for which the game is played. When this is done his opponent may, at his option, give up, surrender the stake and commence a new game, or he may accept the double and proceed with the game.

When the opponent accepts the double, he has the sole right to double the stake a second time and may do this at any time before any of his throws. This in like manner gives the initial doubler the option of surrendering the stake, already once doubled, and commencing a new game, or of accepting this second double and continuing the game.

When the initial doubler accepts this redouble, he has in like manner the sole right to double the stake a third time and may do this at any time before any of his throws.

Continuing in this way, there may be also a fourth double, a fifth double, and so on, in theory, indefinitely; although, in practice, there are rarely more than four or five doubles in a game.

As we have indicated, the privilege of doubling is at first with either player. It then alternates, being always with the player who has accepted the last double.

As will be readily appreciated, this new element has tremendously increased the possibilities of backgammon. Repeated doubling means an increase of the original stake in what is known as arithmetical progression, which means practically by leaps and bounds. The first double makes the original stake 2 and the second double makes it 4:. This does not seem so formidable. However, five doubles make it 32 and ten doubles which, though possible, can very rarely happen, will make it 1,024. Twenty doubles, which are unheard of, would make it 1,046,576.

In addition to this doubling of the stake, in this game gammons or double games are preserved, but not backgammons or triple games. That is, upon winning a game, if the adversary has not taken off a single man, the player wins double the amount of the stake, whatever that may be at the close of the game. For example, if the stake has been doubled to 2, redoubled to 4, and the player wins a gammon or double game, he scores 8.

The possibility of such an enormous increase in the original stake may seem at first sight to involve a more conservative player in too great a hazard. However, this is not the case for, as the right to double alternates, the original stake can never be increased by more than one double without the voluntary cooperation of both players. And, against even the initial double, a player is afforded perfect protection by being permitted to decline the double, forfeit the original stake, and commence a new game.

In this doubling we have accordingly a unique combination — the exciting possibilities of a game of poker in which the sky is virtually the limit — being approached by arithmetical progression — and protection when desired against anything more than a single double or the loss of a single stake.

We believe no other game includes such exciting possibilities for the venturesome and at the same time such protection for the conservative. Poker, with a substantial limit, or with no limit at all, has perhaps equal possibilities, but what protection has a poker player against raises in the ante or in the opening, or against raises in the betting by two or more others which may continue indefinitely, notwithstanding a limit to the amount of each bet?

It is hardly necessary to mention whist in this connection. In that game the possibilities have been always limited and there has never been any protection against an inexperienced or stupid partner. In the modern game of “Contract,” the lack of any such protection is only emphasized by the increased importance of possible disasters, and the increased possibility of their occurrence, because casual players of games can hardly be expected to master the complicated conventions necessarily involved.

In addition to its exciting possibilities, modern backgammon can always be social and even convivial. Unlike so many other games, there is no occasion for burdening the memory or for serious mental concentration. It is unnecessary even to preserve silence, always so depressing socially. The disturbing presence of the fair sex and the distraction of charming conversation, so little appreciated by players of the more laborious games, is never unwelcome. In fact not only the players themselves may converse freely, but every one else also, provided, of course, no plays are suggested.

While on the subject of conversation, we might point out that in this game conversation by the players themselves may be almost an art in itself. There are doubles which it is advantageous to have accepted, and there are other doubles which it is advantageous to have the opponent decline and surrender the game without the risk of any further play. And, of course, the disposition of the opponent to accept or decline a double depends generally to some extent upon the manner of its presentation conversationally or otherwise.

As in salesmanship or poker, this involves a psychological study, the practical problem being to “sell” the unwary opponent a double which he should not accept or “bluff” him into a surrender when he has still a reasonable chance.

There can never be any question as to the fairness of this, for in backgammon it is utterly impossible to actually misrepresent the situation, or to lead or mislead any one. It is a game which is always literally “open and above board.”

The further elaboration, known as chouette, has been another fortunate addition to the game and its possibilities. By means of it, backgammon need no longer be limited to two players, but may be played by three, four, five or any reasonable number.

In the French ecarté, a card game for two players, one of the players sometimes made a side bet with one or more of the spectators or, as we sometimes express it, “took an extra.” When this was done, the one playing single-handed was said to be playing “la chouette.” From this the name chouette, for backgammon with three or more players, appears to have been derived.

We shall first describe this game for three players. To commence, each of the three players throws one die and the one who throws the highest number is said to be “in the box.” We do not know the origin of this expression, unless it is borrowed from baseball in which pitchers are knocked out of the box as are players of chouette.

Of the other two players, the one who has thrown the second highest number plays against the player in the box. The third player, who has thrown the lowest number, sits to one side and is temporarily inactive. However, this third player, although inactive, is a partner of the second player, having the same interest against the common adversary in the box. If the player in the box loses the game, he loses the stake to the second player, who is actually conducting the game against him, and at the same time he loses an equal amount to the third player who is inactive in the play. In like manner, if the player in the box wins the game, he wins the amount of the stake from each of the others.

It will be readily understood from this that the player in the box, when he wins, wins double; that is, the amount of the stake from each of the other two players. On the other hand, when he loses, he loses double; that is, to each of the others.

If the player in the box succeeds in winning the game, his first opponent, who has thrown the second highest number and played the first game for himself and partner, withdraws and sits to one side, while the third player takes his place and plays the next game for himself and partner against the player in the box.

The game proceeds in this way, the players not in the box each in turn playing games alternately against the player in the box, until that player loses a game. When this happens, the one who has succeeded in defeating the player in the box becomes the player in the box. He continues in the same manner to play against the other two, now partners, until he in his turn is put out of the box by being defeated by one of the others.

During the play it is always permissible for the two players, who are partners against the third in the box, to consult with each other as to plays and doubling and accepting or declining the latter. The inactive partner may freely suggest plays or doubles, but it is not wise to overdo this as too many suggestions are apt to be confusing and prejudicial.

Whenever there is a difference of opinion among the partners as to the play, the active partner, who is playing that game, must decide what play shall be made. The active partner also must decide when to double the stake. The inactive partner may not do this independently.

The question of accepting or declining doubles made by the opponent in the box, must also be determined by the active partner. However, it is usual, when the partners differ, to permit one partner to decline the double, in which case he loses to his partner the amount of the stake at that time, while the other partner accepts the double and continues the game, assuming-individually the risk of a double loss and the possibility of a double profit.

For more than three players chouette is played in the same manner, the additional players being additional inactive partners who may be consulted and make suggestions, have the same interest in the game and in turn play the common adversary in the box, until he is dislodged by being defeated, when the partner overcoming him plays in the box in his turn against all of the others.

In chouette, with more than three, the player in the box is accordingly always in a position to win or lose treble, or quadruple, or more, according to the number of players. It will be readily appreciated that this game, with a number of players, and the doubling of the stake, and perhaps double games also, gives the player in the box an opportunity with tremendous possibilities. A successful run in the box may amount to almost anything. On the other hand, there can be no such thing as an unsuccessful run in the box. As soon as the player in the box is defeated, out he goes and his loss, therefore, can never exceed the amount of the stake which he has accepted multiplied, of course, by the number of his opponents. In the nature of things there can never be any real disaster like those tragedies which occur in games such as roulette, when one player undertakes to act as banker and has a prolonged run of bad luck.

While chouette, as a game, includes almost unlimited possibilities, its possibilities socially seem to be equally great. As it may be played by any number, there is never any difficulty about a new arrival joining the game, nor is a game ever broken up by one of the players being obliged to leave. Moreover, in this game silence, as we have already pointed out, is unimportant. Memory and mental concentration are unnecessary and all pleasant conversations, commenced at dinner or elsewhere, may be continued.

Returning, as we promised, to observations upon the relation of this game to the present-day conception of youth, its singular appropriateness must now be more or less apparent. It includes all modern youthful virtues or vices, whichever they may be regarded. The game requires no knowledge of science or of the arts and hardly any mentality beyond that pleasant quality which we still prefer to designate by its proper English name, “alertness.” Nowadays this is generally referred to as “pep” and seems to be in fact the only quality necessary to the fulfillment of our modern ideal of social life.

There is also the excitement of an unlimited game and the illusion at least of taking unlimited chances, so fascinating to youthful cigarette smokers, while actually the danger of anything tragic can generally be avoided. In this game there is always action. The more rapid the moves the better and there may be unlimited noise. Indeed, if the rattle of the dice is drowned by ukuleles, water whistles or saxophones, radios, Victors or a whole jazz orchestra, this can hardly affect the players or the outcome of the game. Where there is no mental concentration there can be no distraction.

Before concluding this chapter, we must mention one more recent development in connection with doubling. This is known as the automatic double. As already described, the right to throw first is determined by each player throwing a single die. Now it sometimes happens that the numbers thrown are the same, in which case the players must each throw the dice again to determine who shall make the opening play.

When this occurs, some players regard this as an automatic double, and the original stake is then doubled before the game is commenced. It may also happen that the same number may be thrown a second time, a third time or more, before the right to play first is determined. Upon each of these occurrences, the stake is again and again doubled before the game is commenced.

We are not inclined to regard favorably this new development. It seems to us to destroy the protection which a player otherwise always enjoys against an increase in the stake, unless by doubling or accepting a double he voluntarily participates in bringing about the increase. It seems to us that, theoretically at least, an unlimited succession of automatic doubles might be forced upon him.

However, some players find automatic doubles amusing, and one of our leading players has made a remark concerning this innovation which we suspect of being a bon mot. In fact, if subjected to any “black crow” inquiry, we would explain that our “idea in bringing up” this subject of automatic doubling was solely because of this remark. Without it “we shouldn’t have mentioned it.”

By this labored introduction, having detracted as much as possible from our rival’s quip, we now present it. It was to the effect that the adoption of the automatic double had proved a truly wonderful thing, because it had introduced an element of luck into a game which hitherto had been so purely scientific!

Chapter IV

Further About The Game And Its Paraphernalia

The board, as we have seen, is made up of four tables of six points each, the six points of each table corresponding to the six numbers upon each of the dice. It is so simple that one might perhaps acquire complete knowledge of it at a glance. However, we do not propose to pass over this important item of our paraphernalia without some comment.

The points upon the board are colored alternately in two colors to enable us to sec the plays more readily. A man moved an even number must necessarily be placed upon a point of the same color as the point vacated. If moved an odd number it must be placed upon a point of a different color. Also we can only hit a blot with an even number when it is upon the color moved from and, with an odd number, when it is upon a different color.

In moving the men one does not count the point from which the move is made. Accordingly a move from one side of a table to the other, a distance of six points, requires a throw of five only. A throw of six would necessarily carry the man into the adjoining table. In like manner a move from one side of the board to the other, a distance of twelve points, requires a throw, not of twelve, but of eleven.

Moves in different directions, when observed in connection with the points upon the tables, show results which may appear peculiar to beginners. For example, a move of three from the six point of one’s inner table places the man upon the three point. On the other hand, a move of three by the adversary, in the opposite direction from the one point in the same table, places the man upon the four point. The explanation of this peculiarity, if it appears to be such, is the difference between subtraction and addition. Six minus three equals three, while one plus three equals four.

In playing backgammon, the style and construction of the board or table is important. The sides and bar should be only slightly higher than the tables; sufficient to keep the dice and men upon the tables, but not so high as to make it difficult for a spectator or a partner in chouette to see readily the position of all of the men. The bar should not be too narrow and the sides should be fairly wide to provide a place for the men when they are taken off. It is an excellent plan to continue the sides all the way around the tables so that there will be spaces for the men taken off in front of each player also. This wide margin about the tables prevents men being dropped upon the floor.

In constructing a backgammon board the size of the tables must be appropriate to the size of the draughtsmen used. When all six points of a table are established, the men must fit in the table. This fit, however, must neither be so loose that there is uncertainty as to the position of the men, nor so tight that it interferes with free and rapid movement. Tables which are in width six and one-half times the diameter of one of the draughtsmen are about perfection. It seems to be a mistake to have too small a board. We believe that larger tables, larger men and also larger dice, make the game more enjoyable.

We have dwelt somewhat at length upon the subject of the board because it is important, and also because most of the backgammon boards generally on sale in the stores are such truly deplorable affairs. We can think of nothing more atrocious than those boards with high and narrow sides, which fold and disguise themselves as two volumes, presumably to mask with scholarly appearance some guilty passion for innocent play.

Unlike the board, the dice are by no means simple. No one knows their origin and yet, since the dawn of history, they have been always the same. Cubic in shape with the numbers one to six so placed upon the six surfaces that the sum of the two numbers upon opposite sides is always seven. Apart from the number seven which, in itself, has such significance, it impresses us as extraordinary that it should have been possible to arrange six simple numbers upon the surfaces of a cube with such a unique result.

It is impossible to make comparisons between things of totally different classes. We cannot compare a Rembrandt to an Hispano-Suiza, or Hamlet to the Holland vehicular tunnel. In forming an estimate of anything we must necessarily confine ourselves to things of its class. Judged correctly in this way, it is difficult to conceive of anything ever made by man more remarkable than a single die. Since its invention thousands of years ago, there has been no invention of its class approaching it and there has never been any improvement upon the original invention.

“Nonsense,” we hear the unregenerate exclaim, “that is only because there is nothing in precisely the same class with dice.” And if this be the explanation, it is the more remarkable still. We can think of no other human product that has been able to maintain a sui generic position and remain in a class by itself for more than fifty centuries!

But we have not expressed the half of it. Familiarity with most things is supposed to be destructive of admiration and respect. When the aborigines first beheld the white discoverers arriving in ships with white billowing sails, they fell upon their knees in wonder. Once they became acquainted, they were wielding contemptuous tomahawks and scuttling the ships. In like manner, our ancestors prostrated themselves in abject terror at the appearance of a little electricity in the clouds. Now we grind it out in millions of kilowatts, enslave it and switch it on and off with a single finger.

With dice it is totally different. Familiarity with dice, instead of breeding contempt, engenders a profound respect and the greater the familiarity the greater that respect. Or perhaps it is more correct to say that with dice familiarity is impossible. They can do the most unexpected things, sometimes most delightful and sometimes most exasperating, without rhyme or reason which we can comprehend.

In fact a mere superficial study of the dice almost annihilates our faith in the generally accepted philosophy of cause and effect. It makes us wonder if those old Greeks were not right in maintaining that there was at least one thing more in heaven and earth than is dreamt of in our philosophy. Τνχη, or chance, having an objective existence and being the true source of all uncaused phenomena.¹

And so to understand dice, we must all become tychismists, or masters of accidentalism. But, until schools are established in which we may become proficient in that subject, we fear we shall know nothing of it, and dice will remain for us forever baffling and mysterious.

Concerning dice, there are, of course, certain facts and figures. These are true enough in themselves and, as they seem to have a relation to the chances one takes or avoids in playing backgammon, a knowledge of them may add to the player’s interest and enjoyment of the game. However, we deny that these facts and figures constitute any real knowledge of the dice. They seem to be merely a part of the old problem of chances and we disclaim any pretension to a comprehension of their practical importance.

There are those, perhaps the majority of our population, who entertain an idea which they confidently assert that, in the long run, luck equalizes itself and that, therefore, in the long run, as a factor in the result, it is nullified and eliminates itself from consideration. This sounds reasonable enough. Furthermore, mathematicians, quite unintentionally, have encouraged a general acceptance of the idea by treating chance as synonymous with probability and expressing the latter in algebraic fraction.

Mathematicians are always taken so seriously and are so very much misunderstood. People speak of mathematical certainties and mathematical demonstrations as if they were the best established and most certain truths of existence. As a matter of fact, mathematicians, as such, are not even interested in truth. It does not concern them. They are interested only in accurate logical thought from given premises. Whether that thought is in regard to fact or fancy is to them quite immaterial. The premises may be true or merely assumed. Even the unknown and unknowable may be assumed and designated by a symbol. By this means, the functions of a logical mind are indulged almost inordinately, whether the subject of thought be the truth, or something so remote from the truth as we know it, that it is beyond our wildest imaginings or power of conception.

But to return, who is there who can demonstrate the truth of the assertion that luck, in the long run, is equal and thus eliminates itself? And who is there who will have the temerity to place a limitation of time to the length of the run required? Even if the assertion were true, if the time required exceeds the duration of the game, or the life of the players, of what practical value is it to any of us?

We do not wish to eliminate any study of probabilities which may add to the interest and enjoyment of the players, nor do we wish to underestimate the importance of understanding all that may be understood. However, we believe it better, like Goethe, to wonder at what cannot be explained, rather than to place too much reliance practically upon unproven general assertion. Should we accept it as a priori knowledge, or as an act of faith, what assurance have we that our reward will not be postponed until we have attained the age of Methuselah, or passed into a second incarnation, when it may be quite unappreciated if not altogether unwelcome?

One of the facts about the dice, to which we have referred, is that with two dice there are thirty-six possible throws. Doublets naturally can be thrown only in one way; that is, both of the dice must show the same number. Mathematically, therefore, the chances against any particular doublet are thirty-five to one.

On the other hand, any other throw except doublets may be thrown in two ways. For example, one die may be six and the other five and we have a six and five. These two dice may also come up conversely, that is, five and six. As this is the same throw and as there are these two ways in which it may occur, we must conclude that the chances against any particular throw other than a doublet are thirty-four to two or seventeen to one.

In order to clarify this, we give below a list of the thirty-six possible throws with two dice and it will be observed that, excepting the doublets, we have counted all of the throws twice, because they may each be made in two ways.

If we add up the numbers included in all of these thirty-six throws, counting doublets double as we do in playing, we find they amount to two hundred and ninety-four. This divided by thirty-six gives 8¹/₆  as the average throw with two dice.

If we wish to ascertain the chances of any given number being thrown by the two dice, we have only to bear in mind that there are thirty-six possible throws and then ascertain in how many of these the particular number occurs. For example, number one occurs in eleven of the thirty-six possible throws and does not occur in the remaining twenty-five. Therefore, the chances of throwing a one are eleven for to twenty-five against.

Reference to the foregoing table will make this clear, bearing in mind that all of the throws, excepting the doublets, must be counted twice, because there are two ways in which they may occur.

In like manner we can readily ascertain that six occurs in seventeen of the thirty-six possible throws and does not occur in the remaining nineteen. Therefore, the chances of throwing a six are seventeen to nineteen. In counting the seventeen we have, of course, included double threes, double twos and all other throws like five and one by which a move of six may be made.

By this simple method all of the mathematical chances in backgammon may readily be ascertained. It is naturally of interest to players, when obliged to expose a man, to know that if exposed to a one or a two, or to any number over six, requiring both dice, the chances of being hit are much less than if exposed to a five or a six.

The following table gives the chances against the numbers from one to twelve being thrown with two dice:

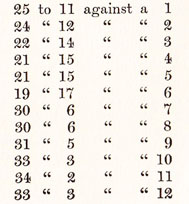
This table assumes that the board is open for every possible throw. Established points intervening reduce the number of throws by which these numbers can be played and lessen accordingly the chances of being hit.

The table shows that, if a blot is left within the reach of one die, the nearer it is placed to the adversary’s men the better. Also that there are long odds against being hit by “double dice,” i.e., upon numbers greater than six, requiring both dice, and especially if ten, eleven or twelve must be thrown.

However, these mathematical chances are by no means conclusive. We do not mean to say that we would bet against them. That would seem to us unreasonably perverse and almost stultifying. On the other hand we feel no security practically in relying, or betting too heavily, upon a mere superiority in the number of favorable chances. A chance is always a chance, if it is only one in a hundred. Experience, which is after all our best guide, teaches us that practical results rarely, if ever, precisely conform to degrees of probability mathematically ascertained. In fact, in actual experience, it seems to be the mathematically improbable that so frequently occurs.

Accordingly who can say that there are not in this, as in so many other things, important elements which we do not comprehend? And who will fail to sympathize with the view expressed by one of our most discerning players, still suffering perhaps from the “bludgeonings of chance,” to the effect that playing backgammon for money is precisely like throwing dice for money, only there is a little more luck in backgammon!

Chapter V

How To Play The Game¹

In the preceding chapters, descriptive of the game, accuracy of statement has been compulsory. Proceeding now to suggestions as to how the game may be played well or successfully, we find ourselves dealing with a subject of a very different character. In regard to it accuracy of statement is impossible. We pass from what has been for the most part statement of fact to what is really matter of opinion.

There are, it is true, certain moves, positions and principles of play so obviously advantageous, in regard to which opinion is so uniform that we feel obliged to accept it as correct. Beyond this what is advantageous becomes less obvious and our subject becomes confused by natural differences of opinion. When it is not clear what is best, there is bound to be individual opinion or preference which, in backgammon, frequently depends upon the degree of conservatism, or optimism, and temperament. Briefly, the personal equation.

However, as our subject is now essentially matter of opinion and must, as we proceed, include our own, as well as that of others, we think we should commence with an express disclaimer of all responsibility. Something like that admirable statement used by bankers and investment security houses would perhaps be singularly appropriate:

“The information herein contained is from sources which we regard as reliable but we do not guarantee it.”

The two most advantageous points to make are the five point in one’s inner table and the bar point in one’s outer table. Accordingly, the best throw in backgammon is double aces and this is played to make both of these points.

The second best throw is double sixes and this is played to make both bar points, one’s own and the adversary’s.²

Double fives are played by bringing over two men from the adversary’s outer table and placing them upon the three point in one’s inner table, establishing that point.

Double fours are played by bringing over two men from the adversary’s outer table and placing them upon the five point in one’s inner table, establishing that point. We believe this to be best, although there are other ways of playing advantageously this excellent throw.

Double threes are played by moving two men from one’s outer table to establish the five point and two men in one’s inner table to establish the three point. Some players prefer to play this throw by bringing over two men from the adversary’s outer table to make the bar point. We prefer the former, because it makes the five and three points. However, it is a close question and, like many of the close questions in this game, could be answered with much greater certainty if we could know in advance what the adversary will throw next. Should he throw double twos or double fours, the first play would block his two men in our inner table and their subsequent escape, with our two points established, would probably be difficult and dangerous. On the other hand, such a throw by the adversary would almost nullify the effect of the second play. The adversary would make the five point in our inner table and that position destroys almost entirely the value of the bar point.

Double twos are played by bringing over two men from the adversary’s outer table and moving two men in one’s inner table to establish the four point.

If the game is commenced by one of the players adopting for his opening play the two numbers thrown to determine the right to play first, and we believe that method to be best, doublets naturally can never be the first throw. They may, however, be the second throw when the original position of the men generally is not materially changed. While the opening play is an advantage, we would prefer to play last if we could be sure of throwing a good doublet. However, the chances against throwing any doublet at all are five to one.

Commencing the game as indicated, we are practically concerned only with opening plays which are not doublets. At this point it may be well to mention that in backgammon it is one thing to form an opinion as to what is the most advantageous move when the men are placed as they are arranged at the commencement of the game, or substantially so, and a totally different thing to determine what is advantageous after the original position of the men has been altered by one or more moves. When we commence the game, neither player has any advantage in position. With every move the position changes and generally becomes unequal and in the new positions which develop other moves may be more advantageous than those which would be considered best with the men in their original position. In fact as we play this game we shall observe that many of the moves we make are not made to establish points or improve our own position, but are made because of opportunities afforded or positions established by our opponent. Nevertheless, they may be the most advantageous under the circumstances.

Excluding doublets, one of the two best opening throws is three and one. This is played by moving one man into one’s inner table and covering it with a man from the six point to make the five point.

The other of the two best throws is six and one, which is played by bringing one man over from the adversary’s outer table and covering it to make the bar point.

The former of these has the advantage of establishing the five point, which is the most advantageous point, while the latter establishes the bar point, the second best point, and at the same time, being a larger number, means more progress and one more man, or “builder,” available to fill one’s inner table. Some players prefer the bar point, but we believe this to be erroneous. The bar point only blocks a six and ceases to be important when the adversary has moved out of one’s inner table. The five point blocks a four, prevents a man that is taken up reentering with a five and also prevents the adversary from establishing that point. This last is important, for the third most valuable point in the game is the five point in the adversary’s inner table. Some writers even regard this five point in the adversary’s table as the second most valuable point.

Six and five is played by moving a man from the adversary’s inner table to the other side of the board, where it is safe upon the same point with the five other men there.

Six and four is played by moving a man from the adversary’s inner table as far as it will go. This leaves the man exposed and some players prefer to play one man into the inner table and another from the six point to make the two point. The objection to the latter is the general objection to crowding one’s game, that is, moving men too far into one’s inner table. Men moved as far as the one, two or even the three point of one’s inner table are practically out of play.

Six and three is played by moving a man from the adversary’s inner table as far as it will go. This leaves the man exposed, but there is no other move worth considering.

Six and two is played by moving a man from the adversary’s outer table to the five point in one’s inner table. This leaves the man exposed and some players prefer to play this throw as a six and three is played. The latter, however, would also leave the man exposed, while the former has the advantage, if the man is not hit, of giving one several chances to make the five point upon the next throw.

We may mention at once to make our consideration of the different plays more intelligible, that in this game we must sometimes voluntarily make blots. Unless the blot is exposed to more than one of the adversary’s men, the chances are always against its being hit. When it is in one’s outer table and can only be hit by double dice, the chances of its being hit are, as we have seen in the table of chances, very remote.

When we say that we should sometimes make blots voluntarily, we do not mean that we should unnecessarily expose men to be taken up and sent back for no purpose and without any reasonable possibility of gaining any advantage. Backgammon is primarily a race to the home tables. To progress more rapidly than the adversary is the primary object and, of course, blots may be taken up and sent back and our progress retarded. However, there are two practical considerations which justify voluntary blots.

The first of these, which is very simple, is when we voluntarily expose a man for the purpose of taking up a blot left by the adversary. Generally speaking, it is always advisable to do this when the adversary’s man, which we take up, has progressed further than the man which we expose. The man so exposed may not be hit and, in any event, the adversary’s progress has been retarded more than our own.

The second practical consideration relates to position. While progress is the primary object of the game, position is of much greater importance in bringing the game to a successful conclusion. Progress without position generally means eventual disaster, while position, even if the adversary has made much greater progress, generally means success. Accordingly, especially in the beginning of the game, when the adversary’s inner table is open and men may readily be reentered, it is advisable in playing certain throws to expose certain of our men to enable us, upon our next throw, to establish the important points necessary to perfect our position and insure, at least as well as that is possible, a successful outcome of the game.

When it is advantageous to leave blots solely for the purpose of perfecting our position is always a matter of opinion. In playing certain throws it is so obviously advantageous that opinion is uniform and we believe must be accepted as correct. For example, double aces, as we have seen, are played to make the five point and the bar point. This leaves a blot which could, of course, be avoided by playing this throw in some other manner. However, the blot left is in the outer table and can only be hit with double dice upon a throw of seven. As the chances against such a throw are thirty to six, our risk is slight and we have established by the play the two most valuable points and secured a tremendous advantage in position. In playing certain other throws the advantage is not so obvious and opinions then naturally differ as to the wisdom of risking blots.

Five and four is a bad throw. It means leaving a blot and offers no great possibilities. Probably the best move is one man from the adversary’s ace point as far as it will go. We like to play the four to the adversary’s five point in the hope of establishing that point upon the next throw, but then a throw of three and one by the adversary will give him the double opportunity of taking up the blot and making his best point, while double threes, fours or fives by the adversary may mean disaster.

Five and three is almost universally played to make the three point in the inner table. We prefer to play this like a six and two, bringing one man from the adversary’s outer table and placing it upon the five point. This leaves the man exposed, but the chances are twenty-one to fifteen that it will not be hit and, upon the next throw, we have several chances of covering this blot and making the five point. Also this avoids placing men as far in the inner table as the three point. Whether or not this unnecessary risk of being taken up is justified is difficult to say. It seems to depend upon how much we should fear being obliged to play a back-game, which subject will be considered later on.

There is only one way of playing a five and two, that is, bringing two men over from the adversary’s outer table. The man moved five is safe and the man moved two may be a useful builder and is only exposed to a six and four, against which the chances are seventeen to one.

Five and one is played by bringing one man over with the five from the adversary’s outer table to safety. The one is moved from the six to the five point in the inner table. The latter is exposed to a four but, if not hit, gives us several chances to make the five point upon the next throw. Some players move the one upon the bar point. This is incorrect, because there are the same chances of the man’s being hit upon that point, fewer chances of covering upon the next throw and the bar point, when established, is not so valuable as the five point. In other words, it is running the same risk for a lesser advantage.

Four and three is a bad throw and there is no satisfactory way to play it. Many players bring two men over from the adversary’s outer table, leaving two blots exposed, however, only to double dice. Other players bring only one man over and move the other number from the ace point in the adversary’s inner table. We prefer to bring over with the four one man from the adversary’s outer table and move the three into our inner table upon the five point. This gives us increased chances of making the five point upon the next throw. Whether or not it is justifiable to increase in this way the chances of being hit and compelled perhaps to play a back-game depends again upon how much we should fear such an eventuality.

Four and two is played to make the four point in one’s inner table.

Four and one is played by bringing one man over with the four from the adversary’s outer table and moving one from the six to the five point in one’s inner table, or, if we prefer to be more conservative, moving one from the ace point in the adversary’s inner table.

Three and two is generally played by bringing two men over from the adversary-‘s outer table. We prefer to bring one man over with the two and move the three into the inner table upon the five point.

Two and one we prefer to play in the same manner. The two from the adversary’s outer table and the one from the six to the five point in our inner table. At least some of the writers upon this game agree that this is the best way to play a two and one, although they do not recommend playing a three and two in a similar manner, which appears to us to be inconsistent.

It may seem to the reader that we are recommending too many plays exposing men in advanced positions unnecessarily. If such men are hit and obliged to reenter, it will generally mean that we are much behind the adversary in relative progress. However, the chances are that the exposed men will not be hit and, if not hit, there is the probability of establishing a strong position, which will protect us to some extent against risks later on, which we are generally unable to avoid and which may be then much more dangerous.

Unless we can always throw remarkable dice, it is impossible to avoid some risks during the course of the game. Every point established early in the game means not only an obstruction to the adversary in playing and reentering, but a safe resting place for some subsequent move. We believe it better to run the risks early in the game, when the adversary’s inner table is still open, and to run them deliberately, leaving the blots which we voluntarily make where the chances of being hit are no greater than they must be, if the blots are to assist in perfecting our position and particularly in making the five point, the importance of which can hardly be exaggerated.

Another important consideration in running these risks early is that it enables us to determine almost at the outset whether or not we shall be able to play a forward game assisted by a reasonably advantageous position. Unless our forward game is to be such a game, it will probably fail, especially if the adversary is equally forward and is about to improve his position by establishing one or more important points. Although our progress has been equally rapid, there is little satisfaction or prospect of success in attempting a forward game without position, against the forward game of an adversary whose position is already well established. If we are to employ only the same strategy we must make our position at least equal, even if we are obliged to run risks to bring this about. Otherwise we can have only a forlorn hope of victory.

If we cannot have a position that is equal, or at least not too inferior, to that of the adversary, we prefer to employ a totally different strategy which is justified, we believe, by the chances of its success and the chances of failure otherwise. We refer to the strategy or method of play known as the back-game. Bear in mind that, in running these risks of being compelled to play a back-game, our other alternative of attempting a forward game without position is by no means attractive. In fact, we believe that under such circumstances the back-game affords us our best, if not our only, chance of success. We shall later on consider this method of play and mention it at this time only in connection with voluntary blots in the opening plays. If we are to be obliged to play a back-game it is of the greatest importance that we should know this at the outset. It is not so difficult to develop a back-game if we set about it early. On the other hand, if the attempt is deferred until we have progressed too far or until our adversary has made a number of points in his inner table, the chances of developing a strong back-game are greatly diminished.

Because of the almost infinite variety in the throws of the dice, there is an almost infinite variety in games of backgammon. There are rarely, if ever, two games alike. However, there are certain types of games with which we become familiar, and it frequently happens that one player will be playing a game of one type, while his adversary is playing a game of another type.

The simplest type or style of game is known as the running game. This is generally attempted when the player has succeeded in getting his men safely out of the adversary’s inner table. He has perhaps made equal or greater progress than the adversary and believes his best chance of winning is to run for his home table. His object is to get all of his men in his inner table as rapidly as possible, at the same time exercising every possible precaution to avoid being taken up.

Another type of game might be called the “shut out” game. This usually occurs after We have made one or more points in our inner table and our adversary has split or separated his men in that table. Now let us suppose that, under such circumstances, we throw doublets and take up one or both of the men exposed in our inner table, at the same time making an additional point or points. It then becomes difficult for the adversary to reenter and, by bringing up additional men, we may again take up the adversary’s men as they reenter and make further points, until we fill our table, the adversary’s men remaining shut out upon the bar while we continue to play.

These “shut out” games, when they can be effected, are generally most decisive victories. They are generally double games and in throwing off there is much less chance of leaving a blot with the adversary’s men upon the bar than when they are upon our one point. In fact, this is such an effective method of winning that, to keep the adversary’s men upon the bar, we should not hesitate to risk blots, even in our inner table, provided the adversary’s table is open.

While these two types of games occur quite frequently, the most usual type or style of game is that of preventing the escape of the adversary’s men from our inner table. This is done by making points in our inner and outer tables, by means of which moves by these men are obstructed or blocked. The primary object of this type of game is to make points, the most important of which are the five point and the bar point. The ultimate object is to establish what is known as a “side prime,” which is accomplished when we have made the bar point and all of the points of our inner table, excepting the one point. This constitutes a perfect block, the adversary’s men upon our one point being unable to move as long as it remains unbroken.

This blocking style of game, in which the obstructing points are more or less completely established, is the most usual game. It has given rise to the saying that backgammon is a game of blocks. Of course, while the points are being made, the adversary’s men are trying to escape. In order to escape, one is sometimes moved forward and exposed. It may then be taken up and additional points made and, if we are fortunate, we may take up the adversary’s other man also and fill our table. Thus a blocking style of game may become a shut out.

These three types of games are all forward games and have three main objectives. To escape and outrun the adversary, to block the adversary’s men with a “side prime” or to take up the adversary’s men and shut them out from reentering by filling the inner table.

In playing backgammon certain principles of play are generally accepted as correct. These include the following:

Make points where they will most effectively obstruct or block the adversary’s men.

When the adversary has advanced his men in one’s inner table making one’s three, four or five point, points in the outer table which will block him are especially important. Only points in front of the adversary are valuable as blocks.

Points which will block the adversary’s large numbers are greater obstacles to him than blocks of small numbers.

When behind and the dice thrown are so unsatisfactory that no play advantageous to oneself is possible, it is advisable to move a man to a position which may be embarrassing to the adversary in playing his next throw. In other words, if one cannot help oneself try and harm one’s adversary.

When obliged to leave blots, leave them where they are least likely to be hit and where being hit will be least prejudicial to the player or most disadvantageous to the adversary.

When two or more of the adversary’s men have been taken up the player should spread his men to increase his chances of making additional points and hitting the adversary’s men when they reenter.

Avoid moving all of one’s men past the adversary’s men unless ahead and the best chance of winning is by running.

In running to prevent a double game it delays the adversary in taking off his men to leave a man or two in his inner table to which his men are exposed.

In running for home the player should use the numbers which he throws to the best advantage. In moving from table to table he should not waste large numbers to accomplish what can be accomplished with small numbers.

When the players’ table is full and men of the adversary are upon the bar, it is best to have the three extra men near the bar as this is safer and gives the player a better chance of taking off these three men before opening his table and enabling the adversary to enter.

The same principle applies when the adversary’s men are upon the one point and, until the table is opened, can only escape with a six. For safety this is then even more important.

In throwing off, when exposed to the adversary’s men, keep an even number upon the point nearest the bar to avoid unnecessary blots.

In throwing off, when not exposed, it is better to have the men spread upon the different points.

In throwing off with a full table and adversary’s men upon the bar, it is generally safer to move up in one’s inner table than to take men off. This permits the adversary’s men to enter, when the danger of being taken up will no longer exist. This policy is always advisable when the adversary is so far behind that a double game is reasonably certain in any event. Otherwise it is a question whether it is advisable to risk; being taken up and perhaps losing the game, for the chance of a double game.

When ahead caution is of increased importance. One has only to retain one’s lead to win. When behind incaution is frequently advisable. Scattered men increase the chances of taking up a blot which may occur, but, when the situation is without reasonable hope, one should not risk blots which may only increase the adversary’s chances of a double game.

We realize, of course, that this statement of moves, positions and principles of play, or of opinion concerning them, may be looked upon as in the nature of advice. With our modern extension of youth, we fear that as advice it is without hope, for we realize also the futility to-day of advice to the young.

In this futility there is perhaps one consoling thought. Our rivals in experience cannot fairly condemn us for betraying them, revealing the secrets of their art and interrupting courses of instruction which may be in progress and the emoluments which are generally incidental if not expected. Besides, if the publication of this book should release from the hag, so to speak, any cats, or even kittens, they are quite as likely to prove in this way boomerangs to us as to those who have a more serious interest in the game or an even more serious interest in what they may regard as the inherent rights and privileges of experience.

Furthermore, our rivals in experience, who entertain ideas of a scientific knowledge of this game, rely upon mathematical probability and regard the play as an art, can hardly fail to appreciate that this book, although not so intended, is practically, from their viewpoint, excellent propaganda for unwary beginners. It cannot fail to bring some converts to our abiding faith in the goddess of chance. From the viewpoint referred to could anything be more helpful? But it is almost proverbial that fortune smiles upon beginners and personally we would rather have their doublets than a science or art which fails to consider, because it cannot comprehend, the important element which might explain their occurrence.

Chapter VI

The Back-Game And Doubling ¹

As we have seen, the origin of dice is lost in antiquity and we do not know the origin of backgammon. In like manner, we do not know the origin of the back-game. All we can say of this is that, just as dice must have existed long before backgammon, so backgammon must have existed long before the back-game was thought of.

Backgammon appears to us to be, like life, a product of evolution from an early beginning, which was simplicity itself. Since the “great black dawn of man” the game “odds or even” with pebbles had long been supplanted by the remarkable invention, dice. There were then, of course, no pads or pencils with which to keep the score. Accordingly, parallel lines were marked upon the ground, the flat surface of a log or upon a table, if such a thing existed, and small pieces of wood or bone, prehistoric draughtsmen of these prehistoric gamesters, were moved according to the throws.

Originally this was merely a convenient and ready method of keeping the score of the dice game. However, as the lines came to an end at the end of the table and keeping the score beyond that point was impossible, the game came to be regarded as a race of the draughtsmen to the last line, or off the table.

Later on, instead of an individual race of two draughtsmen, each player was provided with a certain number of these. The game then became a tribal race, but a simple race still, until certain players conceived the idea of taking up single men, or blots, and sending them back to start the race anew.

In this way backgammon was discovered. We may rest assured, however, that nothing so complicated as the back-game ever entered the heads of the first players of backgammon.

The back-game was invented, probably long afterwards, by some experienced and unusually alert player. Whatever was his name or race we do not know, but he added to the play of backgammon a new strategy, undreamt of by the originators of the game, a knowledge of which can only add to our pleasure and interest.

Before the invention of the back-game, the player with the better dice for progress and position necessarily always won. He had to understand, of course, the elementary principles of play, but that was all. Practically this meant that if one player had a few excellent throws, like double ones or sixes, and his opponent had a few dreadful throws, like two and one, the game became too unequal. To the winner even it ceased to be interesting and to the loser it was hopeless.

The inventor of the back-game changed this. His new strategy transvalued the conventional estimate of the value of the different throws, or reversed it. To him a good throw was a bad throw, and vice versa. He applied to backgammon that ancient teaching — the first shall be last and the last shall be first — and he taught us to win games with what we had believed to be bad dice.

Practically, the strategy of the back-game has for its immediate objective going back instead of forward, getting behind instead of ahead and making points in the adversary’s inner table instead of in our own. To accomplish this, instead of avoiding blots, we leave blots and we leave these purposely where they are most likely to be hit.

An excellent method of accomplishing this is to scatter blots in our inner as well as in our outer table, breaking even the six point if necessary. One or two of the adversary’s men are taken up and, as they reenter, taken up again. In reentering or in moving, these men are certain to hit our scattered blots and we find ourselves reentering these and making points in the adversary’s inner table.

Of course, this cannot continue indefinitely. Eventually the adversary’s men escape and proceed towards his inner table. However, if our strategy has been successful and our back-game has developed satisfactorily, we have become strongly entrenched in the adversary’s inner table. This makes it impossible for the adversary to enter properly and fill his inner table completely. His men become crowded upon the few points available, many of his throws are blocked, or partly so, and in throwing off or moving it is generally impossible for him to avoid leaving blots, which we may have several chances of taking up.

Meanwhile we have been returning some of our men to our inner table, making the best points and establishing the best position to retain the adversary’s man or men which we succeed in taking up. We cannot do this perfectly at once, because some of our men are still back, but we do it by degrees as best we can and, meanwhile, scatter other men in the outer tables, so that, should the adversary’s men escape from our inner table, we will have many chances of recapturing them and obliging them again to reenter.

As we proceed in this way, keeping back the man or men which we have captured and progressing and improving our position, we are now playing a forward game. The principles of that game generally apply, modified slightly perhaps by two considerations. It is particularly important to block large doublets because, when these occur, a captured man is afforded the best opportunity to escape. Moreover, we need have little hesitation about leaving blots, because, at the conclusion of a successful back-game, the adversary’s inner table is generally broken and scattered men are apt to be more useful to us in perfecting our position and in preventing the escape of a captured man.

It is practically impossible to make a comparison between the forward game and the back-game or to form a definite conclusion as to which style of game is the more likely to succeed. Many forward games succeed and many back-games also succeed. On the other hand, the most perfect of forward games sometimes results in disaster and the best developed back-games sometimes accomplish nothing.

With good dice it is a comparatively simple matter to commence a perfect forward game and, provided the dice continue good, to play such a game to a successful conclusion. On the other hand, a back-game is never simple in its development or play. Many of our men must be taken up and sent back. Two or more points in the adversary’s table must be secured and there must also be back a sufficient number of men so that, while the adversary is moving or taking off men, we shall not be obliged to advance too far, crowd our men upon the lower points of our inner table or move out of the adversary’s inner table and lose opportunities to hit the blots which the adversary will probably be obliged to expose.

In developing a back-game the greatest difficulty, as well as the first essential, is to get back far enough. To get back sufficiently is the only safeguard against being eventually “ahead of our game,” which in a back-game can only mean failure. In this strategy nothing succeeds like excess. Against too rapid progress later on, the only security we can have is men back which may be moved to improve our position, without defeating ourselves by destroying our position and the value of our strategy.

In the forward game good dice, and a continuation of good dice, seem to be necessary. In such a game there seems to be never absolute security. One bad throw, such as six and five or five and four, and one or even two blots may be unavoidable and the game may collapse.

In a well-developed back-game, while there is always uncertainty that opportunities will be afforded or that we shall be able to avail ourselves of them, once these things occur a successful result seems to be at least comparatively secure. If we block large doublets and scatter our men in the outer tables, it is extremely difficult for the adversary’s captured man to escape. Should we succeed in capturing also a second man, the escape of two becomes almost impossible. At this stage the adversary’s table is generally broken and he is helpless. Even if the two captured men are all he has left upon the board, his chances of winning are not equal. He will frequently decline to accept a double of the stake and surrender without further play.

A back-game well established is always a strong game. Let anyone who doubts this try a few experiments. For example, let him place ten or twelve or all of his adversary’s men upon the one, two and three points of his own inner table. The remaining adversary’s men may be anywhere, provided they are not out of play. Let him then place his own men upon the other three points, the best points of his inner table, or some of them upon his bar point if he prefers, and see who wins the game.

Such an experiment, of course, may only confirm, instead of overcoming the doubts of the player who is sceptical as to the strength of the back-game. He may throw perfect dice and remove his men without exposing even a single blot. However, the chances are that he will not do this. He will probably expose at least one man and to more than one number or chance of being hit. The opportunity of the back-game then presents itself and, if the adversary plays that game correctly, retains the captured man and blocks him until a second blot occurs and a second man is captured, the strength of the back-game will be apparent.

“But,” the sceptical will exclaim, “what chance has any one of establishing such a back-game?” They may also add that, even with such a game, one successful experiment does not prove that the back-game has always the better chance.

The answer is that, although we may not establish precisely the back-game of our experiment, which is more exaggerated than ideal, nevertheless, if we set about it early, the chances are that we shall be able to establish a back-game that is at least to some extent formidable.

Concerning the chances of success with a back-game there is no uniformity or consensus of opinion for our guidance and we ourselves shall not venture one. The sceptical will be right if they say that in this regard one experiment proves nothing. We cannot justly form opinions based upon any individual experiment. Even a number of experiments may prove misleading. However, fortunately we are not constrained to formulate or express an opinion upon so difficult a subject, for it is our view that this is wholly unnecessary.

In playing backgammon we do not have to decide abstractly whether there are generally better chances of success with a forward game or a back-game. It is unnecessary and inadvisable for us to do this, or to attempt to determine in advance which strategy we shall adopt and play accordingly. On the contrary, we must be opportunists, guided in this by the opportunities which our dice afford. Regardless of the relative merits of the two methods and one’s opinion of that generally, it would be absurd in a particular game to attempt either one of these methods when the dice make that one difficult or impossible and are ideally suited to the other.

For example, if a player begins with six and one, followed by double fours, it would be folly for him to attempt a back-game, even if he were of the opinion, as an abstract proposition, that back-games are generally more likely to succeed. With such excellent dice, he would already have too good a chance to win with a forward game to justify sacrificing it for his opinion of the probable outcome of the two methods abstractly considered.

In like manner, if a player begins with unfortunate dice, like two and one, and has accomplished nothing in progress or position, he can hardly hope to succeed with a forward game against another forward game already well established by the adversary. Under such circumstances, there can be little doubt that a back-game presents the better chance of ultimate victory and this without regard to the player’s estimate of the two methods generally.

Whatever may be one’s opinion of the back-game generally, it has certainly a better chance of success against a good forward game, than another forward game which is decidedly inferior in progress and position. The back-game is always at least a last hope or additional opportunity to the player who is throwing inferior dice. With superior dice we should win, but what are we to do with those games in which our dice are decidedly inferior? The inventor of the back-game has given us the answer. By means of his strategy, we are able to win not only those games obviously favored by our share of the luck, but also a certain number of those games in which the luck apparently favors our opponent.

Can anything be more gratifying than this? By our superior skill, we defeat not only our opponent. We also outwit our bad luck and overcome the design of fortune. The player of the successful back-game will certainly accept this view in all seriousness. Should it provoke a smile, this will be only upon the lips of the divinity to whom this book is dedicated!

Once started upon, it is generally advisable to continue with the back-game persistently. There may be occasions when it is possible to change into a forward game. However, one should not be misled into doing this by one good throw, when one is far behind and a forward game will be so unequal that success is improbable.

In addition to learning to play the backgame, one should also learn to oppose such a game when played by the adversary. This game in opposition to the back-game is known as the counter back-game and in this only three methods appear to be known.

The first is to make points in one’s outer table, from the bar point out. This blocks the men which the back-game player has reentered in one’s inner table and compels him to move his other men, which frequently means that he is unable to hold the best points of his own inner table, the men upon these points being obliged to move further in and out of play.

Another method in this counter back-game is to prevent the back-game player from making points in one’s inner table. This is done by taking up his men as they reenter even if this necessitates the exposure of blots. These blots, of course, are sometimes hit and this leads to the third method, which is to retard one’s own game also by having men taken up and reentered and in this way starting a second back-game in opposition to the first.

In addition to these methods there is the obvious method of avoiding taking up the adversary’s men. When this is possible, it is, of course, advisable, because taking up the adversary’s men is generally only assisting him with his back-game. However, it is generally impossible to avoid taking up the adversary’s men, especially when we are obliged to reenter and he has purposely exposed a number of blots in his inner table.

In regard to doubling the stake there is not very much to be said. It will be readily understood that doubling always gives the adversary a potential advantage — he may at any time redouble. As the player who has doubled first may not also do this, the game thereafter proceeds with this inequality; the player who has doubled first must continue to play the game to its conclusion and until then is generally always liable to be defeated by some unexpected reverse or by very unequal dice. On the other hand, his opponent having the right to redouble is not always obliged to risk concluding the game. Whenever there is a change in the game giving him the advantage, he may redouble the stake and this will frequently compel an immediate surrender by the adversary without the risk of further play.

Moreover, doubling only multiplies the original stake by two. Whenever we double we give our adversary the right to redouble, which is a greater privilege, entitling the adversary to increase the stake twice as much, that is, in effect, to multiply the original stake by four. It is also true, of course, that the adversary in redoubling gives one the still greater privilege of doubling back again, which will increase the original stake eight times.

To determine when it is advisable to double is frequently extremely difficult. It is, in fact, generally more difficult than any question concerning the play, and it is more important in its direct effect upon the score. Doubling early in the game is dangerous, because backgammon is peculiarly a game in which the advantage may shift very quickly from one player to the other, and this is especially so in the beginning of the game, before a strong position has been definitely established. At the same time, if we defer doubling until we have too definite an advantage, the adversary will generally surrender and our opportunity of making the game score double will have been lost.

Generally speaking premature doubling should be avoided and premature doubles by the adversary should always be accepted. We believe that early in the game it is generally more hazardous to double than to accept a double. In its early stages it is impossible to foresee l1ow the game will develop and accepting a double gives us at least one definite advantage in the privilege of redoubling.

When we have made the five point and the bar point we have established the foundation of a strong forward game. Unless our adversary is equally well established, we should always double. Our adversary may surrender and deprive us of the double game we might have won. However, the possibility of a double game, which in the early stages of the game is always a remote possibility, is not worth the risk of playing the game to its conclusion, exposed constantly to the many chances of the advantage shifting to our adversary.

Even when decidedly ahead in progress and position, it is better to defer doubling when the adversary is shifting into a backgame. His back-game may develop well and it is safer to double after the game has progressed further and we can be more certain that the back-game will not be too strong for us. When an attempted back-game is not developing satisfactorily, it is generally folly for the player who is attempting it to accept a double, for it is probable that he will lose also a double game. The wisdom of doubling such a game is also often questionable, for this may mean only a surrender by the adversary and the loss of an excellent opportunity for a double game. These questions always involve an estimate of the possible strength of the adversary and of the prospect of a double game. One should not double when the game is secure and there is a good chance of a double game. The adversary may surrender and thank one for insuring him against losing a double game. When the game is insecure it may be better to double and encourage a surrender by the adversary and this is especially so when the prospect of a double game is remote.

When one has a decided advantage and hesitates to double, fearing a surrender by the adversary and a lost opportunity for a double game, it is sometimes helpful to wait until after the adversary has made a decidedly good throw. With such a throw the adversary’s morale is frequently restored to a degree quite unjustified by the actual situation. By doubling then one can take advantage of this misleading psychological effect, for, under such circumstances, the adversary is very apt to accept a double that he would not otherwise consider. The adversary’s throw, of course, must not be so decidedly good that the game is no longer reasonably secure.

As the game approaches its conclusion doubling, when one has the advantage, becomes more and more safe and, therefore, more and more advisable unless there is a good prospect of a double game. The nearer the conclusion of the game the fewer are the remaining throws and the less the chances of the advantage shifting to the adversary. Therefore, with only a slight advantage and many throws remaining, a double is hazardous and one should generally accept such a double.

In throwing off, when the game nears its end, unless there is a prospect of a double game one should always double when one is only slightly ahead. One should then use a double to force a surrender without risking any further continuation of the game and possible large doublets by the adversary. Near the end of the game, under such circumstances, the adversary generally will surrender and he should do this unless he is indeed a tychismist, or master of accidentalism, and can disregard mathematical probability and throw the necessary doublets. And, we may add, we have seen this done by persons who generally try to pass the occurrence off and excuse themselves by claiming to be possessors of what they describe as a “hunch.” Notwithstanding their excuses, such persons, if not in fact tychismists, must be regarded as suspects and should be excluded from all games of chance.

At the beginning of this chapter we referred to evolution. In considering the origin and development of the game we believe this was appropriate, but one would hardly imagine that any connection existed between evolution and the play of the backgame. Nevertheless, when an exaggerated type of back-game was being developed, with many blots voluntarily exposed, one of the bystanders, who are frequently veritable kibitzers and only too apt to appreciate comments more than back-games, described this style of play as the Darwin theory, an effort to make monkeys of them all.

Chapter VII

The Laws Of The Game

In games as in governments laws are generally an interference with natural freedom. Their only justification is practical necessity. In the one case, practical necessity for the good of the game and the players. In the other, practical necessity for the welfare of the State and its citizens.

In a State there should be some guarantee against unnecessary legislation, and some provision for the automatic repeal of laws whenever the necessity or reason for their enactment has ceased to exist. In this country, unfortunately, we have neither of these things and accordingly our laws are annually increasing at a rate which foretells a bulk that will be appalling.

So far as this growing hulk is concerned, the disposition of our legislators seems to be always to add, and rarely, very rarely, to subtract. We are commenting upon this, not condemning it, for this disposition is a natural one. When we elect a man to a State or to the Federal legislature, he becomes a legislator and naturally desires to function as such. He is not elected to reform and perfect our laws as a whole and very probably is not qualified for that.

We need a Moses, a Lycurgus, a Solon or a Napoleon, but until one appears, having the authority as well as the wisdom, there seems to be no prospect of relief. The bulk of our laws may assume the proportions of the Great Pyramid of Ghizeh, but, like other obvious imperfections in the practical working of our excellent heritage, a problem is presented with which one hundred and twenty million self-governing people are apparently unable to cope.

In the regulation of games we have fortunately no similar difficulty. The Solons of the different games generally make the rules as a whole and, from time to time, revise them in the same manner. This is the ideal method and the results are excellent. Instead of an ever increasing bulk which becomes more and more unintelligible, we have an intelligent effort for perfection — reduction to the simplest possible form and the elimination of everything unnecessary. In Utopia legislation will surely be conducted in this manner, unless indeed, in Utopia no laws at all are necessary.

In the game of backgammon, excepting perhaps the unknown inventor of the backgame, there have been no outstanding players. To-day there appears to be none such and no acknowledged champion or recognized authority. In this, as in other respects, backgammon is unique, but the practical result is that there are no real Solons of this game to make and revise the rules by which we play.

There is Hoyle, it is true, but Hoyle was a general authority and this is an age of specialists. We have been obliged long ago to realize that, notwithstanding our limitations, knowledge has increased beyond the capacity of any one individual. Over a century ago Hoyle presented himself to a then unsuspecting public as an authority upon all games just as, at an earlier date, Sir Francis Bacon declared all knowledge to be his province. We do not question the sincerity of these gentlemen, but we cannot to-day accept their pretensions as within the limits of the humanly possible.

We cannot to-day accept the original Hoyle, or any of his successors, as a Solon of games in general, and it is not surprising that we should find it impossible to accept in their entirety the thirteen laws laid down in the most recent Hoyle for the game of backgammon.¹

Some of these laws might properly be a part of the description of the game, others are unnecessary, while still others are preposterous. For example, there is no necessity for requiring the players to announce their throws and it is unnecessary and also annoying to oblige a player to move a man because he has happened to touch it.

The seventh law of this Hoyle provides that, if a player interferes with his dice, his opponent may compel him to play any numbers the opponent may choose. This is preposterous. We do not believe it possible that the dice can be controlled by interference, certainly not by accidental touching, and there is no occasion for so severe a penalty.

The thirteenth law is also unduly drastic. It provides that, if a player throws off men before all of his men are home, the men thrown off must be reentered in the adversary’s table. The correct view, it seems to us, is that mere accidents should never be so severely penalized. If the occurrences are not accidental the game should be discontinued.

The following of these rules are excellent and are generally accepted.

Each player must throw the dice into the table on his right hand, and if either die jumps into the other table, or off the board, both dice must be taken up and thrown again.

To constitute a fair throw, each die must rest flat upon the board, and if either die is “cocked” against the other, or against the edge of the board, or of a man, both dice must be taken up and thrown again.

If a player moves a man the wrong number of points, the adversary must demand that the error be corrected before he throws. Otherwise it may not be corrected, unless both players agree.

We would like to make the last a little more general. We think it should require the adversary to demand the correction of any and all errors before he throws. This would cover throwing off accidentally before the men are all home. Furthermore, there should be the following additional rules which are also generally accepted.

A play is regarded as completed when the move or moves required by the dice are made correctly and the man or men quitted. After a play has been so completed it cannot be changed.

If a player throws his dice before his adversary’s play is completed, the throw is void and he must throw again.

As in backgammon there are no Solons or recognized authorities, there seems to be no way in which the rules can be definitely established until there is some day assembled an international convention of the players. Meanwhile, let us hope that the players, acting as Solons individually, will eliminate everything unnecessary and reduce what is essential to its simplest possible form.

Chapter VIII

Conclusions Of A Backgammonist

We release “backgammonist” as a new word to be added to our language. The addition must be necessary for we find nothing in the dictionaries having the meaning we desire to convey.

We cannot say “backgammon player,” for that would imply a proficiency which we do not possess and an interest primarily in the game itself. To us, it is true, the game is delightful. It seems to possess inherently qualities which stimulate, without exhausting, one’s natural passion for play, and its “infinite variety,” like the charm of the Egyptian queen, is never staled. Nevertheless, our interest in the game amounts to little. Such an interest, which we might have had, has been entirely lost in the much greater interest which we have in the players and in our own reflections, which we shall endeavor to explain.

For some unaccountable reason opponents at backgammon indulge themselves in mental and emotional activities to an extraordinary degree and far beyond anything that the play of this simple game seems to require. They think they are conservative and wise and possessed of a superior understanding of the game, or they think they are lucky, run quite unjustifiable risks and double the stake prematurely. They invariably think the contest would be ridiculously unequal, were it not for our phenomenal luck, and they carry in their memories for days, to reproach us privately or in public, the good throws we do make on rare occasions, while utterly oblivious of their own.

With different opponents the same play will produce mental reactions which are totally different. For example, a voluntary blot in anticipation of establishing the excellent five point (which players frequently regard as unorthodox although it is approved quite generally) will convince one opponent that we are inexperienced or foolish, or both, while another opponent will become suspicious and regard the play as a trap. In like manner, after we have shown a disposition to play a back-game, one opponent will assist us by taking us up whenever he can, while another opponent will so studiously avoid this that his chances of winning the game are seriously impaired.

But it is emotionally, rather than mentally, that these activities are most pronounced. In fact, these psychical reactions of the players seem to run almost the whole gamut of the emotions. Confident superiority, keen pleasure and triumph are at times manifest, while at other times pathos for our blunders, suspicion, annoyance, disappointment and righteous indignation against what they term bad luck, to them the only possible cause of defeat, are equally manifest and sometimes emphatically expressed.

These manifestations, of course, vary tremendously with different types and temperaments. There are the collected self-contained types who have everything well under control and are generally proof even against calamities resulting from extremely provoking performances on the part of the dice, which occur seemingly in defiance of mathematical probability. However, the most interesting players are those of the perfectly homozygous type, whose every emotion is mirrored in attitude, gesture and facial expression, accompanied sometimes by sounds, not necessarily words of our language, which harmonize perfectly with their emotional state.

The extent of these manifestations seems to be peculiar to backgammon. Possibly this is because other games generally require some distracting mental or physical effort. In backgammon, with neither of such distractions, the free play of the emotions is undiverted and we get results which could not fail to interest a specialist as they are obvious even to laymen and frequently the subject of comment.

In fact, one of our friends, who has observed the game only casually, has been so struck by the expressive countenances of backgammon players that he has suggested that there be included in this book six or eight photographs showing their characteristic expressions, especially in connection with unusual occurrences in the game. These photographs would be arranged over the title “Types of Backgammon Players” and would, of course, include the portrait of a player after his third or fourth unsuccessful attempt to enter a man when the adversary’s inner table is only half closed, and also the portrait of another player who has three men upon the bar, only one point open and throws the appropriate doublets.

Were it possible we would gladly adopt this suggestion, for there can be no doubt that such photographs, if not of interest to players of the game, would be an invaluable contribution to the scientific study of facial expression and of the human emotions.

“The proper study for mankind is man,” said the poet, and we believe backgammon affords for this the perfect opportunity. We are not sure that the poet intended to include in this subject of study those divinely fair creatures that have added to our lives the possibility of romance, but we hope so, for We draw from this the one chord which has been missing and which seems essential to make our book harmonious and complete.

We perceived at the outset that a book on backgammon, while containing little of value about the game (the dice, the truly important element, being ununderstandable) might include incidental references to many other subjects. We saw that there might be references to history, to the classics and to mathematics and possibly thoughts from the philosophers and from the poets, but we never imagined that it would be possible to include romance.

However, what cannot a backgammonist accomplish and why should he feel restricted by ordinary human limitations? Any natural gift of alertness, cultivated by the play of this game, should develop into something truly great and wonderful and would readily see a connection and relevancy that might escape the eye of an ordinary mortal.

As the play of this game never distracts from an absorbing interest in the players, in like manner fortunately it never distracts from one’s own reflections. One may play this game and at the same time think of life as it is or dream of life as it might be. And if the ancient and mysterious cubes with which we play suggest something beyond our comprehension or experience, why not let them suggest that ideal which, through the ages, has been always fancy’s highest flight? παραδεισος, or paradise, that wonderful garden or remote region in which the faithful are blessed with rewards eternal and

Even the etymologists can tell us little or nothing of the origin of the word paradise. Like the origin of dice it seems to be buried in the remote past. The ideal it signifies is no more elusive than the pair o’ dice with which we play and who can say they are not both derived from identical roots of some lost prehistoric tongue?

At all events, we can play this game, think of our ideal and dream of our most wonderful inspiration to the true romance.

FINIS

More book transcriptions