Backgammon FAQ: Match Play

Backgammon FAQ

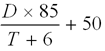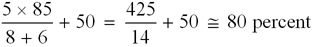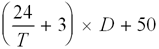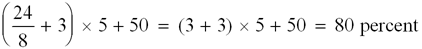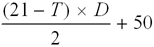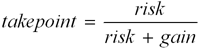
Match Play

Introduction
Match Equity Tables
Learning Match Equities
Using Match Equities
Post-Crawford Play
2-away 2-away

Q: What is match play?

When backgammon tournaments are held to determine an overall winner, the usual style of competition is match play. Competitors are paired off, and each pair plays a series of games to decide which player progresses to the next round of the tournament. This series of games is called a match. Match play is also popular on backgammon play sites.

Matches are played to a specified number of points. The first player to accumulate the required points wins the match. Points are awarded in the usual manner: 1 for a single game, 2 for a gammon, and 3 for a backgammon. The doubling cube is used, so the winner of each game receives the value of the game multiplied by the final value of the cube. Automatic doubles, beavers, and the Jacoby rule are not used in match play.

Q: Does it matter how much I win by?

No, there is no advantage in winning more than the required number of points. Your sole goal is to win the match.

Q: What is the Crawford rule?

If you are playing a match up to n points and one player reaches n − 1 points, the Crawford rule says that the doubling cube is out of play for one game. This one game without doubling is called the Crawford game. After the Crawford game, the doubling cube is back in play again. The Crawford rule is a standard part of match play.

Match to 5 Score
White Black

Game 1: White wins 2 points 2 0 Doubling Allowed
Game 2: Black wins 1 point 2 1
Game 3: White wins 2 points 4 1
Game 4: Black wins 1 point 4 2 Crawford Game
Game 5: Black wins 2 points 4 4 Doubling Allowed
Game 6: White wins 2 points 6 4

In this example, White and Black are playing a 5-point match. After three games, White has 4 points, one short of what he needs for the match. That triggers the Crawford rule, and no doubling is allowed in the next game, Game 4.

The idea behind the rule is that without restrictions on doubling, the player who is behind in the match would double at his first opportunity every game. This reduces the number of games needed to win the match, lessening the value of the points held by the player who is winning. On the other hand, if the cube were taken out of play completely, the player who is behind in the match would have to win all his remaining points without any help from the doubling cube at all. The Crawford rule is an intelligent compromise. See this post by Walter Trice.

The Crawford rule was devised by John R. Crawford, coauthor of The Backgammon Book. See this post for more information.

Q: What is the Holland rule?

The Holland rule was popular in the 1980s, but is rarely used today. The Holland rule says that after the Crawford game a player may not double until his third turn of the game. The idea was to try to create more skill in cube handling in post-Crawford games. The rule never really accomplished what it was designed to do, and has now been discarded. See this post by Kit Woolsey.

More Information

Match Equity Tables

Q: What is a match equity table?

A match equity table is a chart that tells your chances of winning a match from a given score. Here is an example:

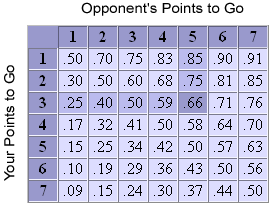
Match equity tables are expressed in terms of each player's points to go. Suppose you are leading 2-0 in a match to 5. We say that you are 3-away and your opponent is 5-away. The same away score would apply if you were leading 4-2 in a match to 7, or 6-4 in a match to 9, etc.

According to the chart, if you are 3-away and your opponent is 5-away, you have a 66% chance of winning the match.

Q: What is the Woolsey-Heinrich match equity table?

The Woolsey-Heinrich table is the most famous and widely used match equity table. It was created by Kit Woolsey using data from matches recorded by Hal Heinrich. The chart was published in Inside Backgammon in 1992, and in the book How to Play Tournament Backgammon in 1993.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 .50 .70 .75 .83 .85 .90 .91 .94 .95 .97 .97 .98 .98 .99 .99
2 .30 .50 .60 .68 .75 .81 .85 .88 .91 .93 .94 .95 .96 .97 .98
3 .25 .40 .50 .59 .66 .71 .76 .80 .84 .87 .90 .92 .94 .95 .96
4 .17 .32 .41 .50 .58 .64 .70 .75 .79 .83 .86 .88 .90 .92 .93
5 .15 .25 .34 .42 .50 .57 .63 .68 .73 .77 .81 .84 .87 .89 .90
6 .10 .19 .29 .36 .43 .50 .56 .62 .67 .72 .76 .79 .82 .85 .87
7 .09 .15 .24 .30 .37 .44 .50 .56 .61 .66 .70 .74 .78 .81 .84
8 .06 .12 .20 .25 .32 .38 .44 .50 .55 .60 .65 .69 .73 .77 .80
9 .05 .09 .16 .21 .27 .33 .39 .45 .50 .55 .60 .64 .68 .72 .76
10 .03 .07 .13 .17 .23 .28 .34 .40 .45 .50 .55 .60 .64 .68 .71
11 .03 .06 .10 .14 .19 .24 .30 .35 .40 .45 .50 .55 .59 .63 .67
12 .02 .05 .08 .12 .16 .21 .26 .31 .36 .40 .45 .50 .54 .58 .62
13 .02 .04 .06 .10 .13 .18 .22 .27 .32 .36 .41 .46 .50 .54 .58
14 .01 .03 .05 .08 .11 .15 .19 .23 .28 .32 .37 .42 .46 .50 .54
15 .01 .02 .04 .07 .10 .13 .16 .20 .24 .29 .33 .38 .42 .46 .50

Q: What is the Mec26 match equity table?

The Mec26 table was compiled by Joseph Heled and popularized in a 2003 article by Albert Silver. Heled use a program written by Claes Thornberg. He set the gammon rate to 26% (thus the name) and supplied his own post-Crawford equities. Mec26 performed well against other match equity tables in computer simulations.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 .500 .685 .750 .818 .842 .892 .909 .936 .946 .962 .968 .978 .981 .987 .989
2 .315 .500 .595 .664 .737 .795 .835 .869 .896 .919 .935 .949 .959 .969 .975
3 .250 .405 .500 .571 .646 .710 .758 .800 .835 .867 .890 .911 .927 .942 .952
4 .182 .336 .429 .500 .575 .640 .694 .739 .781 .817 .847 .872 .894 .912 .927
5 .158 .263 .354 .425 .500 .567 .623 .673 .720 .761 .796 .827 .853 .876 .895
6 .108 .205 .290 .360 .433 .500 .559 .612 .662 .706 .746 .780 .811 .838 .861
7 .091 .165 .242 .306 .377 .441 .500 .553 .605 .652 .694 .732 .766 .797 .824
8 .064 .131 .200 .261 .327 .388 .447 .500 .552 .600 .645 .685 .722 .755 .785
9 .054 .104 .165 .219 .280 .338 .395 .448 .500 .549 .595 .637 .676 .712 .745
10 .038 .081 .133 .183 .239 .294 .348 .400 .451 .500 .547 .590 .631 .669 .703
11 .032 .065 .110 .153 .204 .254 .306 .355 .405 .453 .500 .544 .586 .625 .662
12 .022 .051 .089 .128 .173 .220 .268 .315 .363 .410 .456 .500 .542 .582 .620
13 .019 .041 .073 .106 .147 .189 .234 .278 .324 .369 .414 .458 .500 .540 .579
14 .013 .031 .058 .088 .124 .162 .203 .245 .288 .331 .375 .418 .460 .500 .539
15 .011 .025 .048 .073 .105 .139 .176 .215 .255 .297 .338 .380 .421 .461 .500

Q: What is the G11 match equity table?

The G11 table was compiled by Robert-Jan Veldhuizen in 2004 using computer rollouts to determine actual win rates when Gnu Backgammon played itself at various match scores.

1 2 3 4 5 6 7 8 9 10 11
1 .500 .681 .751 .818 .845 .890 .909 .936 .946 .961 .968
2 .319 .500 .600 .672 .746 .802 .844 .877 .904 .925 .941
3 .249 .400 .500 .574 .650 .714 .765 .809 .843 .874 .897
4 .182 .328 .426 .500 .577 .646 .702 .749 .791 .828 .857
5 .155 .255 .350 .423 .500 .568 .629 .680 .727 .769 .804
6 .110 .198 .286 .354 .432 .500 .563 .618 .670 .716 .756
7 .091 .156 .235 .298 .371 .437 .500 .556 .610 .658 .703
8 .064 .123 .191 .251 .320 .382 .444 .500 .555 .605 .652
9 .054 .096 .157 .209 .273 .330 .390 .445 .500 .550 .599
10 .039 .075 .126 .172 .231 .284 .342 .395 .450 .500 .549
11 .032 .059 .103 .143 .196 .244 .297 .348 .401 .451 .500

Q: Which table is best?

If you assume perfect play by both sides, then the G11 table is probably best, though we don't know for sure. But the G11 table only goes out to 11 points. If either player has more than 11 points to go in the match, you have to use a different table.

For human-versus-human play, the Woolsey-Heinrich table may be best because it is based on the results of actual matches, though some of the matches in Heinrich's database are 20 years old or more so they may not accurately reflect modern play. The Woolsey-Heinrich table is easier to learn than the others, but it only provides two decimal places of precision; sometimes you need more than that to make correct match-play decisions.

The Mec26 table performs very well in computer simulations. This may or may not make it a good table for human-versus-human competition. One advantage of Mec26 (and other tables computed mathematically) is that you can extend them as far as you like. It is also easy to incorporate into a computer program.

Practically speaking, any reasonably accurate table will do.

More Information

Learning Match Equities

Q: What is Janowski's formula?

Rick Janowski devised a formula to help learn the Woolsey-Heinrich match equity table. Suppose the trailer is T points away from winning the match, and D is the difference between the leader's score and the trailer's score. Then the leader's match equity in percent is approximately

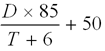
For example, if the leader in the match has 3 points to go, and the trailer has 8 points to go, the leader's match equity is

Q: What is Turner's formula?

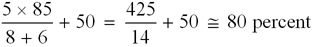
Stephen Turner came up with formula which is easier to calculate than Janowski's formula. Suppose the trailer is T points away from winning the match, and D is the difference between the leader's score and the trailer's score. Then the leader's match equity in percent is approximately:

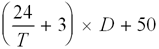
For example, if the leader in the match has 3 points to go, and the trailer has 8 points to go, the leader's match equity is

Q: What are Neil's numbers?

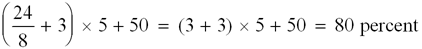
Neil Kazaross has a method of estimating match equities using the following chart.

Trailer's Points to Go 3 4 5 6 7 8 9 10 11 12 13 14 15

Neil's Number 10 9 8 7 6 5 4

Take the difference in the players' scores, multiply by the appropriate Neil's number, and add 50 to get your match equity in percent. For example, suppose the leader in the match has 3 points to go, and the trailer has 8 points to go. The difference in the scores is 5; the trailer's Neil's number is 6. Multiply 5 times 6 to get 30, add 50, and you get 80 percent winning chances for the leader.

Q: What is the Muench Formula?

This formula is discussed by Danny Kleinman in ... But Only the Hogs Win Backgammons. Suppose the trailer is T points away from winning, and D is the difference between the leader's score and the trailer's score. Then the leader's match equity in percent is approximately

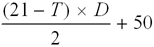
Muench's formula is not as accurate as the others for longer matches, and should be used only if both players have 11 points to go or less.

Q: What about 1-away?

None of these formulas works well when the leader is 1-away (Crawford). These are the equities in the first column and first row of a match equity table. You'll just have to memorize those.

Comparison of Match Equity Formulas

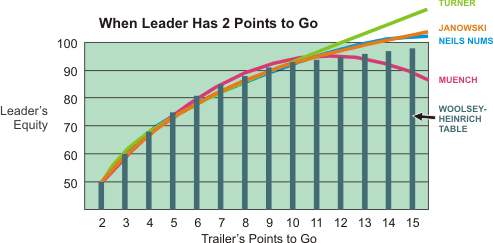
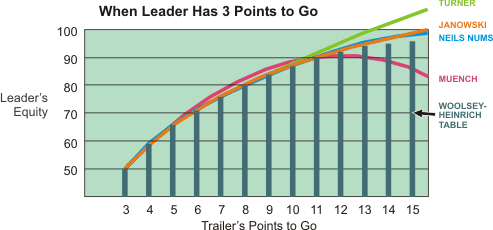
More Information

Using Match Equities

Q: What is my take point?

Your take point (sometimes called your "point of last take" or "drop point") is the minimum chances in the game at which you can still accept an offered double. It is the break even point between taking and dropping.

Your take point depends on the score in the match and the level of the cube. For example, the trailing player at 4-away 2-away is much more willing to accept a double than the leading player. That is because he can immediately redouble and put the entire match on the line with one game.

Take points are often computed without regard to gammons and recube potential, so the money-play take point is 25 percent. (To see why 25 percent is the money-play take point, imagine playing four games and being offered four cubes. If you win one out of those four games—25 percent—your total loss is the same whether you take every cube or drop every cube.)

Q: How do I calculate my take point?

The easiest way to work out your take point is by computing a risk-reward ratio. This is best illustrated with an example. Suppose you are leading in a match 3-away 4-away and your opponent doubles you. How good must your chances in the game be to accept this double? There are three steps in the calculation:

CALCULATE THE BASE: The first thing to do is find out what your match equity is if you drop the double. In this case, your opponent gets one point and the match is tied, so your match equity is 50%.
CALCULATE THE RISK: If you take and lose 2 points, your opponent will now lead the match 3-away 2-away. The W-H table says your match equity at that score is 40%. So you are risking 10%, the difference between the 50% above and 40%.
CALCULATE THE GAIN: If you take and win 2 points, you are now leading the match 1-away 4-away. The W-H table says your match equity will be 83%. So you gain 33% by taking.

Your risk-reward ratio is 10 to 33 — you risk 10 points to gain 33. In money play, the break-even risk-reward ratio is 1 to 3. Here, your risk-reward ratio is lower than that, so you can accept more readily that if playing for money.

You can calculate your exact take point using the formula:

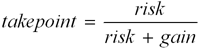
In this case, risk/(risk + gain) = 10/(10+33) = 10/43. Your take point at this score is about 23%.

Q: What about gammons?

When your opponent has a chance of winning a gammon, this must be factored into your calculation. Suppose in the example above that half your opponent's wins are gammons. Let's redo the risk calculation to see how this affects your take point.

CALCULATE THE RISK: If you take and lose 2 points, your opponent leads 3-away 2-away and your match equity is 40%. But half of your losses will actually cost 4 points and a 4-point loss gives a match equity of 0%. Your average match equity after a take and a loss is therefore 20%.

This changes things completely. Now you are risking a whopping 30 points to get 33 points. This means you have to be much more careful about accepting opponent's double.

Similarly, when you have a chance of winning a gammon, those gammons should be factored into your risk-reward calculation as well.

Q: Is all this calculation really necessary?

The answer really depends on the individual. Some people are able to memorize a match equity table and do the necessary calculations easily in their head. Others find it impossible without making a mistake. Often you can figure out the correct cube action by comparing the match situation with money play. Ask yourself:

What are my chances and my opponent's chances of winning a gammon?
Can I realize the full value of my gammon wins if I double and he takes? (E.g., if you double when you are 2-away, and opponent takes, your gammon wins will now have no extra value.)
Can I realize the full value of my recube if I accept a double? (E.g., if you accept a double when you are 2-away, you gain nothing by recubing.)

There are still times when the only way to figure out the correct cube action is to go through all the calculations. But those situations are relatively rare and many people play a high level of backgammon without doing precise calculations at all.

More Information

Post-Crawford Play

Q: What is a "mandatory double"?

If you are trailing a match, and your opponent is 1-away, and the Crawford game has already been played, you have nothing to lose by doubling. That is because if you lose the game you'll be losing the match anyway. You might as well play the game with the cube at 2. Since you risk nothing by doubling, a post-Crawford double is called a mandatory double.

Q: What is a "free drop"?

If you are leading 1-away 2-away after the Crawford game, your opponent will surely double you. (See "mandatory double" above.) When he doubles, you have the option of accepting the double and playing the current game to decide the match, or declining the double and playing the next game to decide the match.

Playing a new game makes the match a 50-50 proposition. So the question you should ask is: What are my chances of winning the current game? If you have less than 50 percent chance of winning the game, then you should drop the double and start a new game. If you have more than a 50 percent chance in the game, take the double and play the game for the match.

This is called a free drop because, whether you take or drop, you are playing one game to decide the match.

Q: What is "the trick"?

Suppose you are leading a match 1-away 3-away, post-Crawford. Your opponent could double right away, but instead he waits. The game evolves into a long race with him now a 90% favorite to win. Finally he turns the cube. Do you accept?

With only a 10 percent chance of winning the game, many people would drop this double. But that would be a mistake. Look at the two scenarios:

If you drop, the score becomes 1-away 2-away, post-Crawford. Next game, your opponent will double immediately and you must either take the double and play that game for the match or drop the double and play the following game for the match. Either way, your chances are about 50% (say 51% because of the free drop).
If you take, you still have a 10 percent chance of winning the game. Plus, if you lose the current game, you have a 50% chance of winning the next game. Your overall chances are 10% of winning the current game + 90% of 50% of winning the next game, a total of 55% chance of winning the match. That's 4% better than if you had dropped!

More Information

2-away 2-away

They don't know the correct cube stategy at 2-away 2-away.
They are waiting for a chance to lose their market before doubling. This is also an optimal strategy, but it takes a sharp eye to see all market-losing sequences.
They hope, by waiting, to induce an error from their opponent. There are two ways you might gain by waiting: (1) Your opponent might drop a double he should take. (2) Your opponent might fail to double before losing his market. The 2-away 2-away score is often a contest of which player is willing to take the greater risk.

More Information