Introduction

When to Double By Phil Simborg (2005). One of the best players in the game, Kit Woolsey, taught me what I consider to be the single best tool for winning backgammon: Woolsey's Law. When you are trying to decide whether or not to double, put yourself in your opponent's shoes. Ask if you are sure he has a take or sure he has a pass. If you are not sure of either, then double! Introduction to the Doubling Cube By Paul Money (2006). It is never too soon to learn cube play. Why? Because if your cube action is good, you will be able to survive in quite strong company. The reverse is not true. Poor cube play will see you destroyed by clever cube handlers. Be a PRAT By Alan Webb (2000). In his book, Improve Your Backgammon, Paul Lamford uses the acronym PRAT as a guide to doubling and accepting. PRAT stands for Position, Race And Threats. Lamford recommends doubling when you have an advantage in two of three areas. And a clear advantage in all three means your opponent should pass. Doubling Cube Strategy By Hank Youngerman (2002). You will never be successful at backgammon if you don't know proper cube play. Many beginning and intermediate players play like they're afraid of the doubling cube. In my experience, beginning players tend to take much too often, and intermediate players tend to drop much too often. Idiot's Guide to the Doubling Cube By Phil Simborg (2008). The idea of the cube is to allow either party to double the stakes of the game. Instead of playing for $1.00, you can raise the bet to $2.00 or force your opponent to quit and pay you the $1.00. Here's a quick introduction on how the cube works in backgammon. The Best Way to Make Tough Decisions By Phil Simborg (2008). Regardless of your skill level, I have one suggestion that will help you make tough decisions, and it doesn't matter whether it is a checker play decision or a cube decision: Put yourself in your opponent's shoes. The Doubling Rule By Kit Woolsey (1991). Reprinted from Inside Backgammon in 1991, this is the original exposition of Woolsey's Law for Doubling. Woolsey's Law states: If you are not 100% sure that the position is a take, then it is always correct to double. Threading the Needle By Kit Woolsey (1999). How the doubling cube can affect checker play. Players sometimes say "I would have made a different move if the cube had been in the center" or something like that. Do they have any idea what they are talking about, or is it just rationalization?. Reference Positions By Kit Woolsey (2001). How do we make our cube decisions? Our judgment is mostly based on experience, from positions we have seen before. The best approach is to understand several common types of positions and know whether they are passes or takes and by how much. Then, when we see a position over the board, we can relate to a similar position which we know. We make adjustments for the differences, and come to a conclusion. Reference Positions By Hank Youngerman (2000). In this article we will discuss the general idea of reference positions. If you can find these break-even points and remember them, you will have taken a huge step toward improving your game. Reference Positions By Phil Simborg (2008). Great players have a huge library, in their head, of reference positions. Having such a library requires not only an excellent memory, but first they must have spent time looking at key positions and committing them to memory. Cube Handling By Tom Keith. Articles on the strategy and theory of cube play. From the Backgammon Galore Forum Archive. Is It a Take? By Kit Woolsey (1984). You can use your ability to assess a pass or take to help determine whether or not to double: Get up, walk around to your opponent's side of the board, and see how it looks to him. Then, answer the simple question: Is It a Take? If there is some doubt, you should definitely double. Six Reasons Not to Double By Kit Woolsey (1982). Most players when faced with a potential doubling position will simply mull the position over in their mind. Then if they like the position enough they will double; if not they will wait a roll. Too often this approach leads to a missed cube opportunity. The Intermediate Cube By Ted Barr (1980). Knowing when to accept or decline a double is the essential measure of skill among backgammon players. Some players' theory of doubling is to accept the cube only when you are the favorite, and to offer it only when you are winning the game. Anyone who believes this theory is naive. Eliminate Emotional Influence By Gaby Horowitz and Bruce Roman (1981). Anyone who has ever played a game of backgammon in a more sophisticated manner than aimlessly moving checkers about a board has experienced the magnitude and severity to which the game can affect one's emotions. Doubles and Redoubles By Oswald Jacoby and John R. Crawford (1970). An introduction to doubling in backgammon. "We don’t know who first added the doubling feature to backgammon, but we feel we owe him a great debt. Without the doubling feature, few people would be playing backgammon today." (From The Backgammon Book, Chapter 7.) The Diabolical Doubler: Betting for Blood By Bruce Becker (1974). There is nothing quite so evil as the smile on a player’s face when he throws the doubling cube at his opponent. Except the cube itself. (From Backgammon for Blood, Chapter 9.) The Doubler By Barclay Cooke and Jon Bradshaw (1974). The introduction of the doubling block is a relatively recent innovation and has added an extraordinary new dimension to the skill of backgammon. The doubler is the key to backgammon. (From Backgammon, the Cruelest Game, Chapter 6.)

Cube Theory

The Doubling Cube  By Peter Bell (1995). I'd like to share my thoughts on how to handle the doubling cube in money games. I'm hoping beginners and intermediates may find this information useful. If you are a strong player, you already know everything I have to say! Optimal Doubling in Backgammon By Emmet Keeler and Joel Spencer (1975). This paper shows that the optimal betting strategy for a continuous model of backgammon is to double when you have an 80% chance of winning. We discuss the differences with the published literature on the real game and the problem of infinite expectations. The optimal strategy for a simulation of the endgame is computed by dynamic programming. On Optimal Doubling in Backgammon By Norman Zadeh and Gary Kobliska (1977). The concept of an effective doubling number for noncontinuous games is introduced. Computer simulation is employed to determine an extremely accurate strategy for accepting, doubling, and redoubling in running games. Take-Points in Money Games By Rick Janowski (1993). This article presents a model of doubling in money games which allows for gammons, backgammons, the Jacoby rule, and beavers. Danny Kleinman checked through this work and acknowledged it as the most accurate model to date. Cube Handling In Backgammon Money Games Under a Jump Model By Mark Higgins (2012). A variation on Janowski's cubeful equity model is proposed for cube handling in backgammon money games. Instead of approximating the cubeful take point as an interpolation between the dead and live cube limits, a new model is developed where the cubeless probability of win evolves through a series of random jumps instead of continuous diffusion. Doubling Theory By Kit Woolsey (1999). How can we determine if it is theoretically correct to double? Although this article is theoretically oriented, some understanding of the concepts involved will be of practical value for making doubling decisions at the table. Doubling Theory and Market Losers By Hank Youngerman (1999). The goal of doubling and taking or dropping is not to "cash" a game that is already all but won, or to show your resolve not give up easily. It is not to end the game, nor to prolong it. The goal of doubling is to increase your long-run expected number of points won per game. Cube Paradoxes By Paul Money (2006). A potpourri of cube-oriented positions with names: the Jacoby Paradox, the Kauder Paradox, and Robertie's position. Doubling the Stakes and Brownian Motion By Jochen Blath and Peter Mörters (2001). This article presents a mathematical model for the doubling cube and calculates the appropriate time to offer a double, and to accept or drop a double, based on the assumption that the players' chances in the game vary continuously. Beaver Theory By David Fletcher (1981). The beaver rule option is commonly employed today, but not much has been written concerning "beaver theory." This article is an attempt to partially rectify this deplorable lack of information. The Double-Beaver Question By Kent Goulding (1982). Looking for a position that is both a correct double and a correct beaver. Everything Is a Take By Jim Pasko (1980). I recently read an article that stated, contrary to common belief, 25% is not the minimum necessary chance to win that justifies taking a double (in no-gammon positions). In at least one case, a 20% chance of winning is sufficient. Here is an example where the chance of winning is just 18.75%! Double-Beaver Revisited By Arthur Ramer (1981). M. Leifer suggested that there exist positions where the correct doubling strategy is to double for one opponent and to beaver for the adversary. The proposed position was subsequently criticized by W. Robertie as not providing sufficient equity for the doubling side. Here is a position meets all the requirements of a simultaneously correct double and beaver. Comments on the Beaver Controversy By Burt Simon (1981). There have been several articles and letters concerning the option of "beavering" a double. The question is whether or not the beavering option would ever be used by skillful players. Some people claim that there are positions where the correct play is to double and then beaver. The Doubling Cube in Money Backgammon By Danny Kleinman (1980). Three basic considerations should govern your cube handling in money backgammon. Most importantly, the backgammon position itself. Secondly, the location of the cube. And thirdly, the nature of your opponents. The Cube Equations By Danny Kleinman (1980). Backgammon theorists have tried to relate proper cube actions to something they call the "probability of winning" the game. But this concept is shattered by the existence of the doubling cube. The cube affects both the frequency of winning and the size of games won. The Doubling Cube and Football Fields By Danny Kleinman (1980). Conceive of a backgammon game as taking place on a football field. Let us ignore the football complications of different numbers of points awarded for touchdowns, safeties, and field goals, as well as the backgammon complications of gammons and backgammons. Winning occurs whenever you move the ball to your opponent's goal line, losing whenever he moves the ball to your goal line. Settlements and Fracture Points By Danny Kleinman (1980). Often your opponent will turn the cube at a "fracture point," a position where the next shake will determine which of two or three divergent paths the game may take. The technique of fracture-point analysis provides fair settlement values for the game as well as sound cube decisions. Symmetry, Marginal Utility, and the Cube By Danny Kleinman (1980). In backgammon, doubling and taking strategies must be considered separately as a rule. Your opponent’s psychology, more than anything else, should determine when you double. But when you should take depends primarily on your evaluation of the backgammon position and only marginally on your opponent’s psychology. Doubling Cube Quiz By Rick Durrett (2003). The doubling cube is common in backgammon but could be used in any game. In this quiz, Durrett looks at using the doubling cube in a simpler game, coin flipping, to see what insights it might give to using the doubling cube in backgammon.

Holding Games

Doubling in High Anchor Games By Bill Robertie (2006). A look at doubling strategy in high anchor games. In almost all normal 5-point holding games, you have a pretty easy take. Your opponent needs about a 15% lead in the pip count to have a good double. More About High Anchor Games By Bill Robertie (2006). Some exceptions to the rule that any 5-point holding game is a take. Low Anchors By Paul Money (2006). Cube handling when your opponent holds your ace-point, two-point, or three-point.

Blitzes

The Blitz By Kit Woolsey (2000). Cube decisions in blitzes can be difficult. It is easy overestimate the danger of the blitz and pass a clear take, or overestimate the defensive chances and take a clear pass. Unfortunately there is no yardstick one can use to measure a blitz position and decide whether or not it is a take. There are a lot of different variables which have to be put together properly to come up with the right answer. Evaluating Blitzes By Bill Robertie (2007). Blitzing positions as a group are probably less understood than any other group of positions. They don't have much of a theory connected with them. Instead, players learn benchmark doubling configurations and their associated values as a guide to assessing positions that arise in actual play.

Going for Gammon

Too Good? Too Bad! By Paul Lamford (2000). How to tell when you are too good to double. For it to be correct to play on rather than cash in a money game, the general rule is that you must have twice as many gammon wins as losses. Playing for the Gammon By Kit Woolsey (2000). The question of whether or not to play on for a gammon can be a very perplexing one. Here are some examples of positions where it is better to play on for another roll than double immediately. Going for the Gammon By Phil Simborg (2007). Some things to think about when trying to decide whether to cube now or play on for a gammon.

Miscellaneous

The Internet Style By Karsten Nielsen (2008). How the rake affects cube decisions when playing online. What Lies Beyond the Board? By Frank Frigo (2006). Efficient doubles are all well and good, but having a strong suspicion that your opponent will pass a proper take, or take a proper pass can be a significant advantage. This suspicion can be derived from their body language or simply from a player's history. Michael's 432 Rule By Michael Bo Hansen (1998). A rule of thumb for estimating your equity after you've been hit and your opponent's board is closed. When "the player with one man on the bar" has 4 men left on his ace point, the probability of "the player with the closed board" winning the game is between 30% and 20%. Initial Doubles By Hal Heinrich (1999). Heinrich looks at positions in the first three rolls of the game where doubling is correct. These are positions we encounter frequently. Volatility By Kit Woolsey (2003). Volatility in backgammon is a difficult thing for us to measure. Yet it is so important when deciding whether or not to double that it must be considered, even if it has to be judged subjectively. Failing to turn the cube in those volatile positions where a lot is likely to happen on the next exchange is very costly. Evaluating Early Doubles By Bill Robertie (2007). When contemplating a middle game double, don't just look at your own position. Remember to look at the weaknesses of your opponent. It may be his weakness, rather than your strength, that gives you a good double. Inducing Cube Errors By Kit Woolsey (2003). If your opponent plays perfectly, you will never have an advantage. You will increase your winning chances if you create situations where your opponent makes errors. When you have a close decision as to whether or not to double, take the opponent's tendencies (to take late or drop early) into account in making your decision. Playing Humans By Phil Simborg (2008). Think about who you are playing and what their tendencies are and what their skill level is compared to yours. If you are playing a human who is less than perfect, and they have specific tendencies (or faults) that are reasonably predictable, you should adjust your game to take advantage of those faults. Doubling the Player By Kit Woolsey (1982). Proper doubling technique involves more than making theoretically correct doubles. It is important to understand your opponent's tendencies to take or pass close doubles in order to make the most of the cube. The Expert's Error By Kit Woolsey (1983). An expert playing weaker competition says to himself: "I am virtually sure to win this match if I can keep the cube low and grind out 1-point victories. Consequently, I will only double when my opponent has a clear pass, and I will never take a double if it is remotely close." This "grind 'em out" approach doesn't work if the weaker opponent is using reasonably good cube strategy. The Doubling Cube in the Wonderland of Errors By Danny Kleinman (1980). Technical analysis can generate optimal taking and doubling strategy against perfectly rational opponents. But we live in a crazy world. You can profit from the irrationality and errors of other players by adapting your own cube handling to their idiosyncrasies. The Cube Provocation Play By Danny Kleinman (1980). Can we then formulate a general rule: "Avoid making plays which get you the cube." For a long time, I thought so. Until a friend wrote showed me an exception.

Pip Counting

The Half-Crossover Pipcount  By Douglas Zare (2000). Knowing whether one is ahead in the race or not is vital for correct playing strategies. Here is a new, simple method for establishing an approximate pip count, which often is good enough. Then when you need it, a few extra calculations gives you the exact pip count. Cluster Counting  By Jack Kissane (1992). Jack Kissane, backgammon master from Albany, New York, is known in many chouette circles as the fastest pip counter in the world. In a June 1989 Chicago Point interview, Kissane claimed that he can count almost any backgammon position within five seconds. Here, Jack Kissane shares his counting techniques with the backgammon community. Naccel 2--aN ACCELerated Pipcount  By Nack Ballard (2010). Naccel is an advanced system of pip counting first described by Nack Ballard in the September 2001 edition of Backgammon Today. In 2010, Nack wrote a series of posts on the BGOnline Forum describing a revised version of Naccel called Naccel 2. This series of 12 articles is taken from those posts. Urquhart Colorless Counting By Robert Urquhart and Phil Simborg (2012). Most of the time all you need is the difference in pip counts rather than the absolute pip counts. This unique method calculates the pip-count difference without even paying attention to the color of the checkers. Coconut Count By Nack Ballard (2017). In order to make half-crossover pip counting faster, I developed the Kangaroo count. When I read about Urquhart colorless counting, it occurred to me that I could supplement Kangaroo count with colorless counting. This new method is called "Coconut count." Cluster Counting Revisited By Dean Gay (2007). As I started using Jack Kissane's Cluster Counting, I began to spot other clusters that are easy to count. Some are just variations on Jack's, but they come up so often I just added them to my "vocabulary." High Fives By Pierre Viau (2011). A pip count method based on counting checkers in each board to get a rough count then making adjustments. Sweet Fifteen By Pierre Viau (2011). A pip count method based on determining the center of gravity for a position, then making mental shifts to create a symmetric position. The Ash Dalvi 13 Count By Ashutosh Dalvi (2011). A pip count method based on identifying checkers or clusters that are multiples of 13. Nack Ballard's Kangaroo Count By Tom Keith (2011). The "kangaroo count" is a variation of the "half-crossover count". It uses a clever scheme to simplify the first part of the half-crossover method where you count octants, or half crossovers, to get a rough count. The Pip-Count of Monte Cristo By Michael Crane (2007). If pip counting is alien to you or you find the mathematics of counting all those checkers on all those points just too much work, then here are some handy shortcuts. Beginner's Guide to Counting Pips By Mark Driver (2000). A description of the "quadrant crossover" technique for counting pips. You start by counting the number of crossovers to get your checkers to their home quadrant. Then you refine the count by noticing where each checker lies in its quadrant. 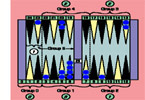Sho Sengoku's Five Count By Sho Sengoku (2001). Advantages of this system are that it takes advantage of the symmetric nature of the board, uses base 5 counting, minimizes arithmetic, requires no "mental shift", is easy and quick to master, and is reliable. Naccel: a[N accel]erated Pipcount By Nack Ballard (2001). In this pip-counting method, you count crossovers and residual pips separately. The crossovers are offset by 1 from the crossovers we are used to. By learning a series of common patterns, called "squads", you can convert multiples of six residual pips into crossovers. Dice Counting, an Alternative to Pip Counting By Grant Hoffman and Jackie Hoffman (2001). This article suggests keeping a running count of the difference between your own pip count and your opponent's. Every throw, adjust the difference by adding or subtracting the playable total of the dice thrown. 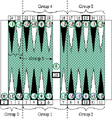General Form for Different Pip Counting Systems By Sho Sengoku (2003). There are some similarities among the three pip counting systems: Douglas Zare's "Half-Crossover Pipcount", Nack Ballard's "Naccel", and Sho Sengoku's "Five Count". Those three systems separate all 26 points of the board in a number of groups, assign a group center, and provide error numbers from the center point to locate any points in a group. 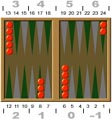The Northern Michigan Pip Count By Robert Townsend (2006). A summary of Douglas Zare's Half-Crossover Pip Count with some shortcuts and tricks to make it easier to use. Counting the Position By Oswald Jacoby and John R. Crawford (1970). An introduction to pip counting written before it was even known as pip counting. "The count represents the total number of points you would have to move to bear off all your men assuming no waste motion." (From The Backgammon Book, Chapter 6.) The Pip Count By Barclay Cooke and Jon Bradshaw (1974). The so-called pip count is an inexact method of determining which side is ahead, and by how much, after all contact between the sides has ceased — that is, when both armies have maneuvered their forces beyond one another and there will be no further contact by either side. (From Backgammon, the Cruelest Game, Chapter 6.) Pip Counting By Tom Keith. Articles on different techniques of pip counting. From the Backgammon Galore Forum Archive.

Match Play

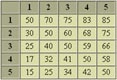Five Point Match  By Kit Woolsey (1999). Woolsey examines every possible score for the five point match and looks at cube and checker play strategy for each score. Introduction to Match Play By Tom Keith (2006). When you play a series of games to a specified number of points, this is called "match play." The article explains all the rules of match play, introduces match equity tables, and provides a brief explanation of how to use match equity tables. The Use of the Doubler in Tournaments By Barclay Cooke and Jon Bradshaw (1974). Tournament tactics differ in many ways from money games and chouette. In tournaments, the only objective is to defeat your adversary, and the difference in your scores is immaterial. (From Backgammon, the Cruelest Game, Chapter 6.) Match Equity For Idiots By Phil Simborg (2008). I have stopped drilling match equity and take points. It just doesn't work for any but highly skilled players. Instead, I teach the concepts to beginner and intermediate players. Close Match Play Strategy By Phil Simborg (2008). Some strategies to employ toward the end of a close match. How does the score affect your checker and cube play? How important is a gammon for you or for your opponent? What can you do to maximize your advantage or minimize your opponent's advantage? An Exercise in Understanding the Match Play Cube By Phil Simborg (2008). Phil leads the reader through the process of a making match-based cube decision. Doubling Cube Study By Phil Simborg (2008). How the price of gammons affect cube decisions in match play. The Backgammon Doubling Cube Made Simple By Phil Simborg (2008). All of a sudden your opponent does something extremely irritating and rude: He doubles you! What do you do now? The Challenge of Tournament Backgammon By Phil Simborg (2007). This article is for people who have enjoyed backgammon on a social level, or playing for small stakes with friends, but are ready to give tournament backgammon, or match play a try. Match Score Explanations By Nack Ballard (2008). There are four match scores that are commonly recognized benchmarks from which checker play strategies for all other scores can be roughly interpolated or extrapolated: Money, double match point (DMP), gammon save (GS), and gammon go (GG). Double? Take? The Mathematical View By Roy Hollands (2001). A quick introduction to doubling decisions in match play. Hollands presents a match equity table and shows how to use it to estimate your take point in various match situations. 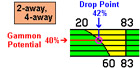Match Play Doubling Strategy By Tom Keith (1995). In tournament play, where matches are played to a specified number of points, proper doubling strategy is different than when games are played for money. This article presents a number of the considerations a player must make when handling the cube in match play. Too Good and Not Good Enough By Tom Keith (2013). One of the strangest phenomena of match-play backgammon is the idea that at certain scores you can be "not good enough to double" and "too good to double" at the same time. How can this be? Staying Ahead By Lasse H. Madsen (2003). How do you protect a lead in a long match; e.g., when the match might still have a long way to go? The focus of this article is on taking doubles. When do you accept an initial double? When do you accept a redouble? Charts show the patterns of how the match score influences take points, and the article develops some general guidelines along with some examples. Crawford and Beyond By Kit Woolsey (1999). In match play, the value of a gammon varies according to the score of the match. This article looks at situations where the correct checker play depends on the score of the match. Post-Crawford Doubling By Matt Reklaitis (2000). How long you can hold off doubling with an odd number of points to go in post-Crawford games. Three-Point Match By Paul Money (2006). In a three-point match, life is a little more complex. Just as in the two-point match, the cube decisions at every score in the three-pointer are different to money play. 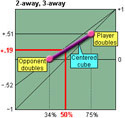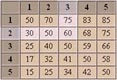Two Away Three Away By Kit Woolsey (2003). Many players have serious difficulties making the adjustments required to their cube decisions at 2-away/3-away. Here are some examples of how to adjust your normal cubing strategy at this match score. Adjusting for the Match Score By Bill Robertie (2007). In matches, optimal play is often affected by the score in the match. The leader becomes more defensive. He wants to reduce the likelihood that the cube will reach a high level, and he wants to avoid gammonish positions. The trailer, on the other hand, is willing to double a little earlier than normal, and perhaps take cubes more aggressively. Only a 4-Cube By Kit Woolsey (2001). You have to be extra cautious when you have a big lead in the match and the cube starts flying. Before sending it over, see how things will look at the level your opponent will be potentially turning it back to. If you do this, you can avoid giving away a match when you are a big favorite to win. The Frozen Cube By Kit Woolsey (2001). This article discusses the concept of a frozen cube, situations where because of the match score one player or both will not want to turn the cube. The concept comes up more often than you might imagine. It is important to look ahead and see what the future ramifications of doubling or not doubling are. Sometimes the conclusions can be very unintuitive. Memoriable Weekend By Kit Woolsey (2002). Some match-play cube decisions from the Chicago Memorial Day Tournament, 2002. Match Equity and Doubling Windows By Hank Youngerman (1999). How to use a match equity table to make correct doubling decisions in match play. The fourth in a series of articles for beginning and intermediate players. Match Play Postings By Tom Keith. Articles about doubling strategy in match play. From the Backgammon Galore Forum Archive. Two-Point Match By Paul Money (2006). In match play, the score is the all-important factor, so let's start by looking at the shortest match length possible, the two-point match. Two-Point Match Strategy By Phil Simborg (2005). Playing a two-point match is a fun and popular game, both on the net and as a side event at tournaments. The interesting thing about playing at this score is that both your cube strategy and checker strategy are different from playing at any other score. And the Trailer Doubles By Anthony Patz (2001). Anthony Patz shows that when both players are two points away from winning the match, it can pay to double even when you are the underdog in the current game. Doubling Windows and Special Doubling Situations By Hank Youngerman (1999). How your doubling varies depending on the score of the match. Special doubling situations: the free drop, 2-away/2-away. This is the fifth in a series of articles for beginning and intermediate players. Match Play at 2-away/2-away By Tom Keith. Articles about the correct doubling strategy when both players both have two points to go in the match. From the Backgammon Galore Forum Archive. A Killer Problem By Bob Floyd (1983). Unusual cube actions when leading a match 2-away 4-away. Cube Decisions at 2-away 4-away By Kent Goulding (1981). For the most part, cube strategy is the same in match play as in money play. However, as a long match nears a conclusion, or in a short match (5 points or less), there are numerous situations where the score compels a total reevaluation of cube decisions. Here is an extreme case that demonstrates the differences between match and money cube strategy. Getting Gammoned? Turn the Cube By Kent Goulding (1982). As tricky as cube decisions can be in money play, in match play they take on a whole new dimension. Someone who plays the cube brilliantly in a money game, but hasn't learned the nuances of match play, is at a tremendous disadvantage. The Fundamental Point By Mike Labins (1982). When leading in the match, be careful about giving the opponent a powerful recube. Cube Critical in Tournament Play By Jerry Nathan (1982). Black was trailing 4-away 2-away when he turned the cube to two. From White's swift acceptance and facial expression, it was obvious that he viewed the double as ill-advised and premature. After all, a two-point game was all that White needed to win the match. The Cube: Tournament vs. Money Play By Barclay Cooke (1980). Backgammon experts are cropping up everywhere these days. But while they become more and more proficient in moving their men, many still don't take time to study the vastly different tactics used in tournaments as opposed to money games, especially in the use of the doubler. Crawford and Beyond By Kit Woolsey (1982). It would seem that once the Crawford game in a match is reached or passed, cube decisions are trivial and checker play is considerably simplified. This is not necessarily the case. An understanding of the intricacies of the Crawford game can give the knowledgeable player that little extra edge which might make the difference. Two Points To Go By Kit Woolsey (1980). I was kibitizing a 15-point match at the European championships, along with Al Lorenz, one of Europe's best players. The score progressed to 13–13, at which point Al whispered to me, "If these guys know what they are doing, the next game should be the last game of the match." Robertie’s Rule of 65 By Bill Robertie (2015). You're playing a 15-point match, and you've got a very comfortable lead, 11-3. You were doubled to two early on, and you took. Now you've broken contact, and you've got a big lead in the race, 26 pips. You'd like to redouble, but you don't know exactly when it's right to do so. The Doubling Cube in Tournament Matches By Danny Kleinman (1980). Match play injects several new variables into cube handling. You must still evaluate positions and react to your opponent’s psychology. But the match score and the cube size assume paramount importance. I hope the strategy I recommend appeals to your reason; it is rooted in calculations based on certain assumptions. Notes on Doubling in Match Play By Bill Robertie (1982). Doubling strategy in match play differs somewhat from doubling strategy in money play. Most cube decisions are the same as for money, but a small number are different. Typically these include doubles beyond the two level, and doubles when one or both players are within four points of victory. Woolsey's Rule in Match Play By Douglas Zare (2003). Woolsey’s rule states: "If you aren't sure whether your opponent has a correct take, you must double." It is very powerful in money play, but it doesn't work as well in match play. Across the Scores By Douglas Zare (2011). When we play backgammon matches, we face a series of decisions at one match score, and then move on to the next score. It is an enlightening exercise to do the reverse: Take one decision, and consider it at several match scores. Dangerous Redoubles By Douglas Zare (2011). Backgammon match play is tricky since the points do not have the same value. It gets particularly interesting when the doubling cube is on 2 or higher, and those decisions are often very far from decisions in a money session.

Match Equities

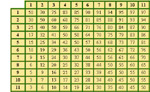Woolsey's Match Equity Table By Kit Woolsey (1999). A match equity table tells you your chance of winning the match at each different score. It is a useful tool in making doubling decisions. Woolsey's table is derived from a combination of empirical data and assumptions about gammon probability and the value of doubling potential. While it may not be totally accurate, the figures should be correct to within a percent or two. The table has proven to be of practical value, and is used by most experts today. 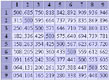Mec26: A New Match Equity Table By Albert Silver (2003). Mec26 is based on a small program published in 1996 by Claes Thornberg. The post-crawford equities were calculated by Joseph Heled using GnuBG rollouts. This table performed very well in comparisons with Kit Woolsey's table, Jacobs's/Trice's table, and the Snowie table. Snowie Equities By Kit Woolsey (2001). Kit compares Snowie's match equity table with his own match equity table and wonders why there is a big discrepancy at the score 4-away/3-away. How to Compute a Match Equity Table By Tom Keith (1995). This article describes how a match equity table can be derived mathematically if you assume a constant gammon rate and efficient cube usage. Lots of diagrams show the process step by step. Match Equities: Simplification vs. Accuracy By Nigel Merrigan (2000). Nigel Merrigan compares three formulas for estimating match equity: Janowski's formula, Turner's formula, and his own Merrigan formula. He finds that his own formula does the best overall while still being reasonably easy to compute. Graphical Match Equity Charts By Sho Sengoku (2003). Using these charts, you can visualize important characteristics of the possible scores in a match. Match Equity Posts By Tom Keith. Various match equity tables and formulas for estimating match equities. From the Backgammon Galore Forum Archive. Committing a match equity table to memory By Fabrice Liardet (2010). Shortcuts are necessary if you want to memorize a match equity table. Here are two separate methods, a very simple one for the Crawford equities, and a more difficult one for all the other equities in the table. Score cards By Fabrice Liardet (2010). Table of take points and gammon values at various match scores and gammon rates. Evaluating Match Equity By Kit Woolsey (1982). In order to assess cube decisions late in the match, it is important to know what your match equity is at the potential scores. The following table is the consensus of independent analyses by Bill Robertie, Danny Kleinman, and myself. Remembering Match Equities By Chris Bray (1997). A match equity table gives you the percentage chance of winning a match at any particular score. The problem is, how do you remember the table? Luckily help is at hand. I shall give two methods by which the match equity for any score in any length match can be calculated. Match Equity Table By Roy Friedman (1989). A computer model developed by the author generates this match-equity table. The primary model parameter is the probability of a gammon in a cubeless game, which has been calibrated from empirical results. Your Table Is Waiting By Jake Jacobs and Walter Trice (1996). If there is a heart to this book, it is Tables 13 to 23. Table 13 is our benchmark table. Use it for any even match up to 25 points in length. It was created by Walter’s program, MEG3, which stands for "match equity generator." Match Equity Formula Reviewed and Revised By Rick Janowski (2013). In 1992, I derived formulae for predicting match equities using the then current match equity tables. I have since been able to derive suitable modifications to my formulae enabling all scores in a 15-point match (including Crawford and Post-Crawford) to be predicted within 0.9% of the Rockwell-Kazaross MET. The Kazaross-XG2 Match Equity Table By Tom Keith (2013). The Rockwell-Kazaross match equity table was a major achievement, obtaining all the match equities for a 15-point match by direct rollout. The Match Score Charts By Danny Kleinman (1980). The next few pages contain charts indicating equities and cube actions in a match to 9 points between opponents of equal skill. Curse You, Norman Zadeh By Danny Kleinman (1983). I spent weeks calculating equities at various scores in a 9-point match and deriving cube strategies from these. I would have been spared all this labor had I known about Norman Zadeh's paper, "On Doubling in Tournament Backgammon," which had been submitted for publication one year earlier. Match Equities into Take Points By Danny Kleinman (1980). Some backgammon players with exceptional memories will learn a complete chart of take points for tournament doubles by heart. But most of us have only limited memories. Can we find some other method of determining how good our chances need be to justify taking the cube at a particular score? The Meunch Formula By Danny Kleinman (1991). Dean Muench, one of the Chicago area's strongest backgammon players, has long sought shortcuts for estimating match equities. Some tournament players have mastered match charts by rote, but in the middle of a match it is better to compute an estimate from a formula than to rely on a memorized chart. Here is Dean's formula. Backgammon Tournament Freebies By Danny Kleinman (1980). When you switch from regular backgammon to tournament play, you must make adjustments. You must adapt your cube handling and checker play to certain special conditions occurring during matches. Here we consider some of these we lump together under the rubric of things that are "free" in backgammon matches. Inside the Database By Kit Woolsey (1992). I analyzed the data from Hal Heinrich's database of over 1000 matches to determine at each score the likely outcome of the next game. From these distributions, I wrote a computer program to generate a new match equity table. The results conform both with Heinrich's database and my own intuition much better than the previous tables. Kit Woolsey’s Match Equity Table By Kit Woolsey (1993). Thanks to Hal Heinrich, we finally have a large database from which we can determine empirically vital information such as likelihood of gammons and the value of cube leverage to the trailer in the match. Using this data, I have constructed a new match equity table. Wrong Match Equity Table By Douglas Zare (2008). Common sense says that if you do everything else right, it shouldn’t hurt much if you use a match equity table which is slightly off. For example, it shouldn’t matter much if you use a match equity table which is rounded to the nearest percent. Mec26: A ‘New’ Match Equity Table By Albert Silver (2003). Joseph Heled, the developer of the Gnu Backgammon neural nets doesn't use the default match equity table shipped with Gnu BG, and instead uses Mec26. No one knew what this was, so he explained that it was based on a small program published in 1996 by Claes Thornberg. The Rockwell-Kazaross Match Equity Table By Neil Kazaross (2010). This is the new match equity table (MET) created by David Rockwell and myself. Rockwell-Kazaross was developed by rolling out every score in a 15-point match almost 39,000 times using GNU 2-ply Supremo. I then carefully extrapolated out to 25 points. Calculating and Using Match Equities By Stephen Turner (1999). In match play, particularly when making doubling decisions, it is useful to know one's match equity. This is the probability that one will win the match from a given score, assuming perfect play by both players. Match Equity Tables over the Years By Tom Keith (2018). A chart of 13 different match equity tables devised over the years and 7 formulas for estimating the match equity at different scores. Users can select different tables from the chart and see how one match equity table compares to another. Rounding Errors in Match Equity Tables By Joachim Matussek (2006). Small rounding errors in match equity tables may cause rather big errors when calculating takepoints. This means you have to use match equity tables with sufficient accuracy to get satisfying results.

Races

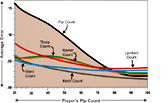Cube Handling in Noncontact Positions  By Tom Keith (2004). A description and evaluation of several popular methods of making cube decisions in noncontact positions. This article introduces the "Keith" count, an accurate formula for making race cube decisions. Effective Pip Count  By Walter Trice (2000). Trice introduces the term "effective pip count" and describes some clever methods of calculating it in different types of positions. In positions where it applies, the effective pip count is a very accurate method of making cube decisions in noncontact positions. The Effective Pip Count  By Douglas Zare (2003). There are several methods for adjusting the pip count to penalize wasteful formations, and the effective pip count (epc) is the best that I have encountered. It not only allows me to assess most races to within a pip, but it provides a framework for learning. An Introduction to the Effective Pip Count By Stick Rice (2007). Introduction the the effective pip count (EPC). End Positions in Backgammon By Edward O. Thorp (1978). Edward O. Thorp examines the proper checker play and cube actions when both players have just one or two checkers left to bear off. Even in these simple games, some very tricky decisions crop up. Thorp provides tables that allow for perfect play, and gives rules of thumb to help players make correct decisions over the board. Curing Your Short Bearoff Blues By Bob Koca (2007). Often a game will come down to one player having two checkers left versus an opponent with one or two checkers left. Since this is common, one can benefit by memorizing a table of these cube actions. This article presents some guidelines to make memorizing the table easier. Cube Handling in Races By Paul Money (2006). Many of our games will end in a race, with no hitting possible and gammons out of the question, so it is important to know how to handle the cube, or we will give away large amounts of our precious equity. The Cube and the Race By Robert Townsend (2007). Introduction to equity and basic concepts of doubling, Woolsey's Rule of doubling, the Jacoby Paradox, and cube racing formulas. The Ultimate Pip Count By Kit Woolsey (1993). In this article reprinted from Inside Backgammon, May/June 1993, Woolsey introduces the concept of a "pipple." A pipple is a unit of measure equal to 1/100 of a roll. Knowing both players' pipple count gives a good idea of your racing chances. Unfortunately, the calculations are quite tedious and "almost certainly not worth the effort at the table". Count Your Pipples By Jean-Luc Seret (2000). "Pipples" is a term coined by Kit Woolsey to represent a time unit worth the 1/100 of a roll. Seret develops a method of estimating a pipple count based on: (1) the numbers of men on each of the 6 points home-board points, (2) the shape of the distribution, and (3) which points have no checkers on them. How to calculate exact game winning chances during bearoff By Joachim Matussek (2004). A linear formula for calculating the EPC for bearoff positions up to 8 checkers is introduced. Two correction terms give an improved accuracy for the estimated EPC. The average error of the estimate is 0.48 pips. The Metric Formula By Nigel Merrigan (2011). The Metric formula (TRICe/MErrigan) is a simple formula that converts the point of last take to raw unadjusted winning chances in percent. (Article revised July 2011.) Cube Handling in Races By Tom Keith. After contact has been broken and the game is a pure race, it is easier to estimate your winning chances and make accurate doubling decisions. Here are some articles on handling the cube in races. From the Backgammon Galore Forum Archive. Can You Take a Double In a Symmetric Position? By Bob Floyd (1981). Some rules of thumb for when to double and when to take in a racing bearoff where you and your opponent have the same position. A Pip Is a Pip, or Is It? By Kent Goulding (1981). A look at a famous bearoff position where both sides have stacks and gaps, trying to decide which side is favored. End Game Doubling: A Science, Not an Art By Jeff Ward (1980). Proper use of the doubling cube is probably the most important and most difficult part of backgammon. One reason it is so difficult is that it is normally hard to prove whether a particular doubling decision is correct or not. There is, however, one important part of backgammon where art gives way to science, and doubling decisions can be determined precisely. Money Cube Action in Low-Wastage Positions By Michelin Chabot (2014). The purpose of this article is to elaborate doubling cube theory in money games for running positions in which there is little or no wastage. The specific purposes are: to present the optimal approach; to analyze three known approaches proposed so far; and to propose a new approach. Improved Cube Handling in Races By Axel Reichert (2014). After looking into how adjusted pip counts and decision criteria work in general, we present a more formal framework that allows us to parametrize and optimize adjusted pip counts and the corresponding decision criteria. The outcome is a new method resulting in both less effort and fewer errors for your cube handling in races compared to existing methods. Analysis of: "Improved Cube Handling in Races: Insights with Isight" By Michelin Chabot (2015). This article explains three flaws in Axel Reichert's "Improved Cube Handling in Races" and comments on other topics of Reichert's article. Finally, the article gives some suggestions on how to further improve the existing theory on cube handling in races for money games. Backgammon Races By Chris Bray (2013). This short monograph summarises the development of formulae for racing situations, the work of other backgammon theoreticians who have led us to where we are today. In particular I must acknowledge the work of Walter Trice. Normal Race Takes By Danny Kleinman (1980). How far behind can you be in a pure race and still have a take? The classic Jacoby and Crawford book simplifies gives a "15% criterion": If your deficit is no more than 15% of your opponent's pip count, you can take his double. All criteria in terms of such a percentage deficit must be inaccurate. They incorporate two different errors — fortunately, errors in opposite directions. Desperate Races and Kleinman Race Count By Douglas Zare (2010). In this column, we'll see a simple, computable racing formula due to Danny Kleinman. We'll use it to analyze a checker play decision which depends on correctly evaluating two desperate races.

Go to:	Next Page of Articles
See:	List of Authors
Return to:	Backgammon Galore

Last updated: 23 Sep 2024