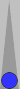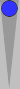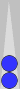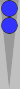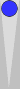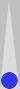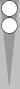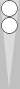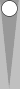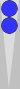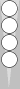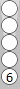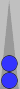This is Part 10 of the Naccel 2 series. In this post, I will discuss the concept of "leftover counts."
With
Naccel, as you have seen, you can freqently count the entire position
in one or two formations, and, unless the count is a multiple of 6
pips, you have some sort of "leftover count." Below is a trivial
example.
The n5 blot requires 5 pips to move/bear in to S0; thus, its count is 5
pips. If, say, your integer count is 3, and you have this n5 blot left
over, your total count becomes 3(5), meaning 3 supes (superpips) plus 5
pips.
Here is a slightly more sophisticated example:
One way to count this leftover blot is to divide the n17 point number
by 6, which is 17/6 = 2 5/6, meaning 2(5). More likely, however, you
currently gravitate towards either
- hopping (+2) the blot forward to reach the previous diagram of 0(5), or
- moving the blot 5 pips out to S2, so that S2 + 5 pips movement = 2(5).
Before long, you will see this blot as an instant 2(5) count; you'll no longer
stutter with (a) or (b). Likewise for a blot anywhere on the board.
Two
blots, or more commonly two checkers on a point, can also constitute a
leftover count. A good example can be found in this diagram in Part 2
(and it is also instructive to see how the 2-pip leftover count was
stripped away and isolated by reading from the beginning of Part 2).
A slightly trickier example is shown below.
To count this leftover two-checker point, you can add 4 + 4 = 8 pips
and convert that to 1(2). Or you can move both checkers −2 − 2 = −4
pips backwards to get two checkers to S1, and count it as 2(−4), same
thing. Or you can divide the point number of n4 by 3 to get 1 1/3,
which again is 1(2).
However, the way I recommend
counting this point is to move both checkers 1 pip forward, creating a
standard pair on n3. The count of that pair is 1, and adding the 2 pips
of motion gives you a total of 1(2). This method is visually clear, and
its advantage in simplicity becomes more obvious the further away from
S0 you move the point. For example ...
Here, you can move the anchor forward 2 + 2 = 4 pips, to get a standard
pair of 5. Therefore, the deeper anchor as diagrammed counts 5(4).
You can handle two blots within a quadrant field in much the same way. Here are two examples:
In
the left-hand diagram, you can move the back blot 2 pips and the front
blot 1 pip (total of 3 pips forward) to get to a pair of 5. Thus the
formation as it stands is 5(3).
For a somewhat more sophisticated example of the above pip-motion finale, look at this diagram (right) in Part 3.
By moving Blue's far side blots a total of 5 pips to the midpoint, a
mirror of 4 is formed, which means that the count of the formation diagrammed there is 4(5).
The
right-hand diagram above is 5(1). There are a number of ways to arrive
at this count, but I find it easiest to move the back checker forward 1
pip to get a split of 5, which is a variant of the pair of 5. Or, if
you don't know/remember the split,
you can move the back blot forward 2 pips and the front blot back 1
pip, netting +1 pips in acquiring the pair of 5. It is preferable to
move in only one direction rather than two, but you can only apply what
you know.
Occasionally,
you might end up with blots in different quadrants. In such cases, you
can hop and shift to a pair (or split or wide). Better yet, you can
shift to a mirror (or mirror variant) or reflection. For
example ...
In
the left-hand diagram, you can move the midpoint blot forward 2 pips to
n5; this creates a (near-side reflection) poof with the blot on n−5.
Therefore, the count of the two-checker formation as it stands
(pre-motion) is 0(2).
You can utilize similar motion on the far side—moving one blot (or point for that matter) to create a far-side reflection (around S2) with another blot (or point), except that it is a count of 2 (instead of 0) per checker.
In
the right-hand diagram, you can move either blot forward 3 pips,
thereby achieving a mirror with a count of 2 with the other blot.
Therefore, as it stands, the diagrammed formation counts 2(3).
Alternatively,
you can view the (right-hand) two-blot formation as half of a (point)
zag; half of 5 is 2½, which is 2(3).
While for the most part during the main count you should confine
yourself to integer counts, you have more leeway in handling leftover counts.
It
is even possible to have a leftover count with three checkers.
Typically, an easy way to deal with them is to move to the nearest
triplet formation. For example ...
This three-checker stack is on an odd-numbered point; that's the bad
news. The good news is that you can either move the three checkers 1
pip (each) forward to form a triplet on n14 (count of 7) or backward to
form a triplet on n16 (count of 8). These two methods are the most
consistent with mainstream counting. However, if you prefer, without
motion, you can forcefully divide the n15 point number by 2. Any way
you cut it, the count is 7(3).
Alternatively,
you can count two of the checkers as a pair 5 and the (peeled off)
spare as 2(3), which adds to 7(3). But (and we'll put aside the motion
alternatives for a moment) it is probably faster to divide n15 by 2.
This example demonstrates that sometimes larger leftover counts can be
a speedier resolution than peeling off all the integer counts available
before dealing with leftovers.
Allow
me to further expand your concept of leftover counts. Perhaps the most
useful leftover formation that is composed of more than five checkers
is the "tween sym." Below are two examples.
In
the left-hand diagram, White has six-checker sym around an imaginary
point halfway between n−4 and n−3. The count, therefore, is halfway
between −4 and −3, which is −3(−3). Because the −3½ point center of symmetry is in between two real points, this formation is called a "tween sym."
In
the right-hand diagram, White has a tween sym centered around her
imaginary 12½ point (where the bar is), located halfway between her
15 and 10 points. This tween sym counts 12½, which is 12(3).
The
most practical leftover counts involve checkers on the midpoint, both
because it is frequently occupied and because it is located just one
pip higher than a Super. Leftover counts of 1(1), 2(2), 3(3), 4(4) and
5(5) are very easy to tack onto your main integer count.
Consider this example:
From the left-hand diagram, you have two ways to quickly reach an integer count:
- You can move the blot backwards 1 pip to create a midtriangle of 5, as
shown in the left-hand diagram below. The count of the left-hand
diagram above is therefore 5(−1).
- You can move a midpoint spare backwards 1 pip to create a midblock, as
shown in the right-hand diagram below. Again the count of 5 minus the
1-pip motion demonstrates that the count of the formation in the
left-hand diagram above is 5(−1).
If
you are still at or near the beginning of your count and choose the
midpoint corner first for whatever reason, employing (a) or (b) with a
1-pip countershift somewhere else is an optimal strategy. But if you've
reached the end and this is a leftover count, you don't have to
worry about carrying around baby pips. Under these commonplace
circumstances, I find the leftover midpoint counts so routine that
instead I tend to move the blot forward, as shown in the
right-hand diagram above. The 4(4) count there plus the 1 pip of motion
means that the formation in the left-hand diagram counts 4(5). [This is
the same as the 5(−1) counted by the back-motion methods.]
Many
examples of leftover counting are illustrated in this post, but I
stress now that you should only apply these techniques to the final formation (i.e., at the end of the count), so that you don't have to carry forward mixed counts only to make another
pip adjustment later—a process that will slow down your counts and
might confuse you. It may be difficult to resist the temptation of a
clever count like a tween sym, but you'll generally do better if you
allow such gems to fall into your lap as leftovers.
Integer
counts are always available, at most one shift away; there's just no
reason to compromise your speed by getting bogged down with fractional
counts and fractional movements mid-execution. If you spend a little
extra time to find large integer count formations and sweep them away,
the nurturing of good habits will reward you with lightning counts
before long.
That said, awareness of how to handle leftover counts is important, and knowing what types of formations you would prefer to save for leftover counts is a valuable intuition to cultivate. Your time reading this post has been well spent.
In Part 9,
I discussed asymmetrical squad poofs.
The most commonly arising tend to involve blocks, pairs, and
triplets.
Below,
I've diagrammed a few more asymmetrical squad poofs (one of which will
shortly appear in a full-board position in this post) in order to
broaden your horizons. S0 checkers have been arbitrarily added. Even if
these exact situations aren't the ones that arise pip for pip, or even
if you only use one side of the squad/squad formation at times, the
more familiarity you have with squads and their variants, the more
shifting options you'll have.
Of
course, as you have seen, poofs, asymmetrical or otherwise, need not
involve squads. Poofs are very efficient formations regardless. Below
are a few examples of sub-squad poofs.
The
formation in the left-hand diagram immediately above is very handy to
remember, because it is also an "asym"—an asymmetrical six-checker
formation around a point (in this case n0). You can slide this
formation (not including the invisible n0 checkers) to the left or right, and/or reverse it left/right and it is always an integer.
In
other words, any formation composed of a point with four checkers plus
a point 3 pips away with two checkers is an integer asym.
It's time to practice counting full board positions. Petter supplies our first:
The key in finding the fastest count for Blue is to attack the biggest
problem area(s) first (typically the checkers that are furthest from
S0) and turn it to advantage. For this purpose, the midpoof is one of my favorite formations.
Having
spotted the midpoof (two checkers each on n7, n−3 and n−4), it is not
terribly hard to find Petter's dual-purpose 2-pip shift (n7 spare
forward 2 pips, n−1 spare back 2 pips):
Two formations can now be easily identified. One is the midpoof (now
stripped of its distracting spare), and the other is a tight
(symmetrical) eight-checker poof around n0. After removing those two
poofs from the board, the only checker you actually have to count is the n5 blot for a count of 0(5)!
Let's repeat the position, with point-numbering from White's perspective:
Again, Petter found the best solution, in my opinion. Without shifting at all,
this position can be broken into two formations, shown below.
The first of the above two formations is a triplet/split poof
diagrammed earlier in this post (with an extra n0 spare). The second
formation, and the only one you need actually count, is a sym around
n2, for a total of 2.
Finally,
let's repeat the main position again, and apply what we know of the
race to determine correct cube action. We'll assume that Blue is on
roll:
Blue has a count of 0(5) or 5 pips. White has a count of 2 (supes) or
12 pips. To get the trailer's (White's) last take point, we can apply
the Nack 57 formula (N57), which I'll restate here:
Add 57 to the leader count, double it, and find the nearest square root.
So, 5 + 57 = 62, doubled is 124. The nearest square root is 11, so that's the take point.
The minimum doubling point is always 3 pips fewer (than the take point) and the minimum redoubling point is 2 pips fewer.
Blue's
(minimum) double point is therefore 8. But he leads by only 7. (That
is, Blue has a count of 5 pips to White's 12). Hence, he should not
double.
The second position is also kindly provided by Petter:
For Blue: Petter, Ian and Jim shifted the n0 spare forward 2 pips,
closing the board. Ian and Peter countershifted a checker in the outer
board (though not the same one) back 2 pips. For the easier of the two
countershift choices, this creates a count of −5 + S1 + 1(3) = −3(+3).
Instead
of a 2-pip countershift, Jim moved the midpoint blot 1 pip forward. His
count is therefore: Closed board −5, S1 × 2 = 2, and motion of +3 pips,
for a net of −3(+3).
[For
negative supe counts, I recommend always prefacing the number of pips
with either a plus or a minus. Otherwise, "−3(3)" could easily be
mistaken as being halfway between −3 and −4 supes (much in the way that
−3½ or −3.5 is interpreted) instead of halfway between −3 and −2
supes. Indeed, the respondent's usages were inconsistent with each
other.]
The closed board is a nice count, but in my opinion it can be improved upon. I got rid of the polarized checkers with this 3-pip shift:
The n5 and n−5 points poof. The sym around n−2 plus the spare on n−3 counts −2(−3).
The
advantage of this shift is that less counting is required and/or in
only one direction. As with the midpoof solution for Blue in the
previous position, poofing the extreme low-count and high-count
checkers simplifies the count.
Note
that other 3-pip back shifts are workable (you might like to
experiment) but I chose this one specifically because it moves one
checker 1 pip and another checker 2 pips (mimicking the forward shift
in the outer board), it separates the other checkers from the (poofed)
n−5 point, and it creates a clear inside count.
Here is the position repeated with point-numbering from White's perspective.
It is tempting to close the board with a few pips (5, in this case),
but once again poofing is faster. The two outer board checkers are
pretty close to n0, but you can still get rid of all four n−1
checkers by applying the asym poof that Petter found and was diagrammed
earlier in this post. After shedding those (as well as the irrelevant
n0 checkers), these six checkers remain:
Here, Petter applied the leftover tactic of the tween sym. These six checkers are symmetrical around an
imaginary point halfway between n−4 and n−3.
The count −3(−3). Brilliant.
If you don't know/remember the tween sym, you can still obtain a
three-prime sym around n−3 by moving the n−5 blot back 3 pips, for a
count of −3(−3). Or, you can similarly create a three-prime around n−4
by moving the n−2 blot forward, for a count of −4(+3).
Here is the main position again:
For bonus credit, see if you can visualize this shift for White: An n−3
checker forward 2 pips (covering n−5), and the n0 spare back 2 pips
(putting a spare on n2). This creates a sock/triplet poof around n0,
and the five checkers on the left are a block of −3 plus the n−3 blot:
again, that's a count of −3(−3).
Ian
took the position a step further, assumed White was on roll, and
figured out the proper cube action. To do so, he converted the leader
count to pips (−3 × 6 − 3 = −21) and applied the Nack 57 formula.
So,
−21 + 57 = 36, twice that is 72. That's closer to 64 than to 81, so the
take point is 8. Blue (the trailer), with −2(−3), is 6 pips behind
White's −3(−3). Ian's assessment is that the potential wastage from
Blue's second n−5 checker costs him another half-pip or so, adjusting
the practical difference to about 6.5 pips. As 6 is already sufficient,
White has a clear redouble. Meanwhile, Blue, who can take even if he is
behind 8 pips, has an easy take being down only about 6.5.
In short, White has a clear redouble and Blue has a clear take. Nice assessment, Ian. I agree.
The third position (White checkers only) is brought to us by Lucky Jim:
This time, Claude is our star. He found this simple but elegant two-checker 2-pip shift:
POOF! The count is zero.
I saw two similar shift-poof solutions (though I missed Claude's), shown below:
POOF! The count is zero in all three diagrams (left, right, and previous).
For
practice, I'm repeating Jim's original position below. See if you can
visualize all three shift-poof solutions. (There are more, but they're
less straightforward.)
Jim said (I paraphrase): "I could see immediately that White has two
checkers on n−5 and four on n−1 for an inner board count of −14 pips,
and she has four on n3 and two on n1 for an offsetting +14 pips. Poof.
Does Nack have any comments this method?" [Jim also offered a second
solution that involves offsetting 12 pips while leaving two checkers on
n−1 and two on n1.]
It
may depend on your exact meaning of "immediately." It appears to me,
Jim, that you're still somewhat (though less so) mired in
checker-by-checker counting, though in positions where the checkers are
close together it's not likely to make much difference.
In my opinion, your second solution (−12p vs +12p) is a slight improvement on your first (−14p vs +14p) because you visually (rather than countingly) cancelled a −2p versus a +2p portion. That's a step in the right direction.
I
definitely find large-scale assaults faster: I search for formations
(poofs especially) with integer counts that involve many checkers or at
least shed extreme ones. I recommend that you practice looking for
dual-purpose shifts and large poofs, and soon you'll be counting faster
than ever.
Go on to Part 11.
| 


![]()