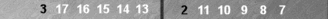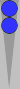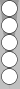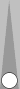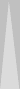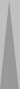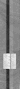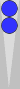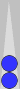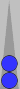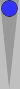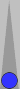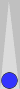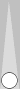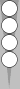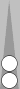This is Part 8 of the Naccel 2 series. I'll start this post by demonstrating a few combined integer counts.
When
checkers occupy Supers, you can't go far wrong counting them as is. On
the other hand, you will so often find one or two checkers on S3 (their
starting location) that it is worth knowing the counts that combine S3's with other common integer formations.
For example, a commonly arising position after 51$-42S-43@ is shown below:
The S3 checker counts 3, and the nearby pair counts 5. This three
back-checker formation is worth committing to memory as an instant
count of 8.
If
you add an S3 checker to Blue's formation, the count of his double
anchor is 11. The larger formation is less common but still occurs
frequently enough that I made a point of learning it.
For a still larger example, see White's five back checkers in this diagram of Part 3.
The S3 point (count of 6) and the n14 triplet (count of 7) coexist
often enough that over time I've learned their combined count of 13
without really trying.
Not
all combined counts need be high-single- or double-digited. In
positions of moderate count, it is typically more desirable to combine
a positive count with a negative count, generating a net integer count
that is zero (best), small positive (second best) or small negative
(third best).
Consider this diagram in Part 4.
The back pair counts 5, and the front pair counts −1; easy enough. But if you combine
them as a mirror of 4, you don't have to subtract 1 from 5: you've saved a step.
Having conveyed the concept, I will now show you some small combined integer counts that frequently arise.
Each of the formations below combines the S3 point (count of 6) with a
sym of
negative count in the inner board. A "sym" (short for six-sym) is any
six checkers symmetrical around a point, though I have chosen to
illustrate the most common sym, the three-prime. (If you don't know how
to count a sym, review the second and third diagrams of Part 2.)
The
four diagrams below are a series. Traditional point
numbers (the purpose of which you'll see in a minute) are added in black under each diagram.
What is cute and memorable about this series is that the traditional
point number ("t") on which the sym is centered is the count of the
formation! In the above four diagrams, the sym is centered on t5, t4,
t3 and t2, making the counts 5, 4, 3 and 2, respectively.
If there is a third checker on S3, add 3 to each of the above counts. If
there is a mere blot on S3 (more likely), subtract 3; for example, you
can count this diagram of Part 7 as t3 − 3 = 0 (among other ways to count it) if you haven't already learned it is a poof.
Next, I will cover "midblot" formations. I'm not
referring to a blot on the midpoint, but rather to a formation with
some number of checkers on the midpoint combined with a blot elsewhere. There are quite a few midblot formations, but the counts are always easy to determine.
Consider this basic formation (which also happens to be a
blot diag).
There is one checker on the midpoint, and a blot on the first point (n−1) in the inner board. [I left a bunch of checkers on S0 to clarify that you skip the Super—you start adjacent to it: at the first (highest) point in the field.] The combination of one and first produces a count of one.
Compare
to the basic formation below. Here the two (midpoint
checkers) and second (the blot is on the second highest point of the field,
n−2) combine to produce a count of two.
Extending the logic illustrated in the last two diagrams:
Three checkers on the midpoint plus a blot on the third point (n−3), a description we'll shorten to "three/third," counts 3.
Four/fourth counts 4. (Four on midpoint, blot on n−4.)
Five/fifth counts 5. (Five on midpoint, blot on n−5.)
Let's build on that knowledge to create similar counts when the blot is in other quadrants. From the formation diagrammed above, hop the blot back one quadrant to the outer board, like this:
In this formation, the blot is in the quadrant where S1 (instead of S0)
lives. Because of S1, you add 1 to the count. Putting the
pieces of the puzzle together, "two/second" (two on mid, with blot on
second point) counts 2, plus 1 (for S1), gives you a count of 3.
To
practice further, let's increase the number of checkers on the midpoint
to four, and therefore slide the blot to the fourth point. (Without
this corresponding slide, the count won't remain an integer).
You have four checkers on the midpoint and thus a blot on the fourth
point. Add one for S1 being in the quadrant, and you get a count of 5.
Getting the hang of it? Okay, let's back-hop this fourth-point blot to the next quadrant:
The blot is still on the fourth point of its quadrant (counting from the S2 Super).
The Blue formation has increased again by one: it is now four/fourth plus S2, for a count of 6.
Let's back-hop the blot one more time:
Blue's count has increased yet again by one. It is now four/fourth plus S3, for a count of 7.
Below, for reference, all twenty possible mid-blot formations
are shown, in five blocks of four diagrams. (These include the midblot
examples already diagrammed.) In each case, the caption reminds you how
to count, and the count itself is repeated on the far right of the
caption line.
If you start with the top left diagram of any four-group and go
clockwise, the counts sequentially decrease by 1, or if you start with
the bottom left diagram and go counterclockwise, the counts increase by
1. Alternatively, if you choose an orientation in the one/first group
and then look at the same orientation in the two/second group,
three/third group, etc., respectively, the counts will sequentially
increase by 1. The more such counting patterns, connections and morphs
of other formations you can spot, the better your understanding of
Naccel and the more sure-footed your counting will become.
[Note: Two of the formations are marked "uncommon." Blue seldom
has a blot on the n2 (trad 8pt) or n0 (trad 6pt) of White, who
occupies these points at the outset of the game.]
I should emphasize that these formations are not vital to
counting in Naccel. However, they will help you imprint other
formations you already know and they are additional tools to help you
achieve lightning counts.
This complete set of Midblot reference diagrams doesn't end the
post. At the bottom there is further discussion, followed by a
full-board position to count for Blue and White.
One/first Midblots
Two/second Midblots
Three/third Midblots
Four/fourth Midblots
Five/fifth Midblots
The formations in the One/first diagram-block have only
one checker on the midpoint, but you can double or triple (etc.) their
size. For example, in the top left "One/first" diagram, the count is 4.
If you put two checkers on each of those points, the count is 8, etc.
The midblot formations in the Two/second diagram-block can be
doubled as well. For example, let's double the patterns in the upper
left and lower left of that diagram-block:
The first of the above two formations, at half size, was originally described as "two/second + S3" = 5.
At full size, we count it as "twice [two/second + S3]" = 10. In a similar vein, the formation immediately above doubles the simpler "two/second + 0" = 2 and becomes "twice [two/second + S0]" = 4.
To become fluent in midblot (and twice midblot) counts, you
need only practice the basic counting technique a little, and before
long what seem now to be methodically plodding counts will become
quicker, then gradually ingrained as instant counts.
Lest you feel overwhelmed by the number of diagrams in this
post, I'll reiterate the point I made earlier: Midblot formations are
not crucial to making fast counts in Naccel. But they will help you
count even faster.
Our choice of feature position in this post is inspired by
a response post from Bill Madison. The position was originally posted here.
Maik and Bill, in counting Blue's outfield, used a neutral shift,
bringing down the four midpointers a pip, and backing up the blot four
pips to compensate: all five checkers meet on S1 for a count of 5.
Petter also recognized Blue's five-checker formation as a count
of 5, though it's unclear to me what counting method he used: "... four
on n7 and one on n2 is 5. I don't know if this formation has a name."
Indeed, it does have a name—it's a midblot! The count is Four/fourth
+ S1 = 5, and after a few times running across this one it will become
an instant 5 in your mind.
To reduce your scrolling, I've repeated the position for Blue below. We will now focus on the count of the left side of the diagram.
Maik, Bill and Petter counted the S3 point as 6, and the n−2 sym as −2, netting a count of 4.
Ian counted the S3 point plus n−3 point as a zag of 5, and the n−1 sym as −1, also netting 4.
I don't deem Maik/Bill/Petter's solution to be better than
Ian's: both are simple two-part counts and it comes down to whichever
you see first. But it is worth noting that Maik/Bill/Petter excluded
the (irrelevant) S0 point. Ian chose to include S0 as a visual aid,
though he could have excluded it by counting the n−2 and n−1 points as a −1 block.)
Is there an even faster way to count Blue's left side? Yes.
Review the S3 point + t4 sym diagram from earlier in this post. When combined with the S3 point,
a sym around t4 (the trad 4pt) yields a count of 4. Blue's left side is
gone in the twinkle of an eye.
I recommend you make Blue's left side an instant "4" in your
repertoire. Because S0 can always be included (even when it's vacant!),
it may be easiest to remember it as: Best four-point board plus deepest anchor = 4.
In short, Blue's entire position can be lightning-counted as 4 + 5 = 9.
Daniel noted that cluster-counting does well in this position:
"For Blue, since one checker on the ace point and two checkers on the
midpoint is 50 pips, two and four are 100. Since a full prime is 42,
Blue's prime is 36. The odd man is 8. Total 144."
Okay, well done;
that's pretty fast for cluster-counting. :)
Moving on, let's repeat the original position and count White:
Daniel and Garyo alertly pointed out that White has only moved 5 pips
from the opening position and therefore the traditional count is 167
minus 5 pips = 162. Likewise for Naccel, 12(5) minus 5 pips = 12. If
you have a convenient reference point, you may as well use it.
For practice, though, let's pretend we didn't get that fortunate. The fastest count without shifting appears to be S3 blot = 3, reflection = 4, midblot = 3, and triplet = 2; total of 12.
[In the above count, note that the reflection
(of n17 + mid)
uses up one midpoint spare, and the other three midpointers plus third
point blot count 4. If you have trouble seeing it, refer to the top
left of the one/first diagram-block and the bottom right of the
three/third diagram-block in this post, the only difference being that
the formations are for White instead of Blue.]
Faster counts can often be obtained with a little shift. My
choice—also spotted by Maik and Petter—is the following 1-pip
shift:
The S3 point is 6, and the double zig is 6, for a total of 12.
Double zig? Yup.
As Maik and Petter found (or remembered), my third paragraph under this diagram in Part 6 states:
"This zig is a combination of a stripped midpoint and stripped
2pt (trad 8pt). Also, as early as the opening roll, a double zig occurs
when an opening 5 is brought down, creating a stack of four checkers on
each point; the entire right side then counts 6."
Recapping, then, for both colors, the count breaks down neatly between the left and right sides of the board:
Blue is 4 + 5 = 9, and (with the 1-pip shift shown) White is 6 + 6 = 12.
Go on to Part 9, or read more below.
| 




![]()