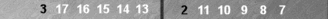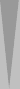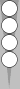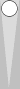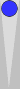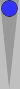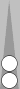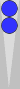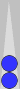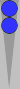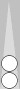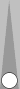|
This is Part 3 of the Naccel 2 series. Thanks to Lucky Jim for his submission, shown below.
Jim informs us this position is from Ballard-Sylvester U.S. Open, June 1989
(though I'll have to confess my memory isn't what it used to be—sigh).
First, let's consider Blue's position. As always, the checkers on the
Naccel 0pt (trad 6pt) are invisible. You need count only Blue's
outfield checkers. These come in two groups, which I'll address
separately.
The first group (shown above) is a six-sym
(six checkers symmetrically arranged around a point—in this case, the 3pt),
for a count of 3.
Jim and Ian nailed this one, perhaps remembering the second and third diagrams of Part 2.
For the other Blue group (see previous diagram, two checkers furthest right
plus two checkers on far side), Ian and Jim shifted the remaining
near-side point one point to the right, and a far side blot 2 pips to
the right to compensate, then moved both far side checkers to S1 to get
a four-stack on S1 plus the 5 pips adjusted. That works, but I'll show
you a faster way.
As a prelude, allow me to present the "mirror."
You could easily count this as two checkers on S2 (Super2), i.e., 2 × 2 =
4, and ignore the two zero-count checkers on S0 (Super0, same as the
0pt).
Alternatively, you can count this as a mirror. A "mirror" can be composed of blots,
points, or even stacks of three or more checkers, as long as they are
of equal size. Mirrors count the same as the total number of checkers
used; here, for example, there are four checkers, so the count is 4.
The only wrinkle to remember is that the near-side member of a mirror is always 1 pip closer to the player's own bear-off tray if one drops the far-side member straight down. (It may help to note that the colors of the points match.)
If we slide the above mirror to the right a few pips, we get the commonly arising mirror below:
Again, there are four
checkers in the mirror, so the count is 4. (To verify the count, shift
both points 1 final pip towards each other so that they meet on S1.
Four checkers on S1 count 4.)
You can probably see where I'm going with this. In the game position, two of the checkers are already on the near-side point of the above diagram. You need only move the far-side checkers 5 pips forward to get the midpoint mirror.
In other words, Blue's entire count has two components. The first is a
six-sym around the 3pt (left diagram below) = 3. The second is a midpoint mirror plus 5 pips (right diagram below) = 4(5).
In short, Blue's count is 3 + 4(5) = 7(5).
Before we count White, I'll reveal another trick. Just as six checkers on a
point count the same as the point number, three checkers on a point
count half the point number.
For example, consider each of White's triplets (three-stacks) below.
The trad 8pt is the Naccel 2-point. White's triplet on her 2pt counts half of 2, which is 1.
The trad 20pt is the Naccel 14-point. White's triplet on her 14pt counts half of 14, which is 7.
After you've seen these triplets a few more times, you'll just
remember them as "1" and "7" without even having to divide the point
number by 2.
Taking special note of White's latter triplet (count of 7), let's go back to the main position:
White's two checkers on S3 (Super3) count 6. Her triplet (as just explained) is
7. Adding those together, White's back checkers count 6 + 7 = 13. [I've
seen this five-checker formation enough times that to me it is simply
"13" (no addition needed).]
For White's near side, remove three of her irrelevant 0pt checkers, leaving
one. Ignoring the outside blot on the (Naccel) 1pt for now, you have ...
This is a six-checker symmetry around the −2pt, for a count of −2.
Now let's revisit Blue's position. I'll remove his 0pt checkers (the ones
that you will learn to ignore), and you pretend that you're counting
Blue for the first time but knowing what you know now:
Blue's count is a six-sym around the 3pt (count of 3) plus a (midpoint) mirror+ of 4(5), for a total of 7(5).
Now I'll remove all but one of White's 0pt checkers (below), and you count
White for the "first" time, knowing what you know now.
White's count is 6 + 7 = 13 in the back, and −2 for the six-sym in her
inner board. Add 1 pip for the outside checker, for a total of 11(1).
Once
you "get" how it works, count both colors in exactly this way a
couple/few more times so that you can get a sense of how fast Naccel
counts are. It's just a matter of knowing a few tricks and spotting
formations.
The difference between 7(5) and 11(1) is 4(−4), or 3(2). That is, Blue
leads by a couple pips more than 3 supes (super-pips)—20 pips, to be
exact.
(If for some reason you want to convert to trad, the counts (with the 0pt checkers added back to the board, of course) are 7 × 6 + 5 + 90 = 137, and 11 × 6 + 1 + 90 = 157.)
[For White's position (after counting S3 × 2), Jim and Ian moved the
three-checker anchor out to S2 (count of 6); to compensate for that 6-pip
adjustment, they moved the two checkers on the −3pt back to the 0pt
(trad 6pt), causing it to disappear. Then they canceled a checker on
the 1pt and −1pt, leaving only blots on the −1pt and −4pt left to
count. This achieves the correct count but is, of course, more work
than counting the three-checker anchor where it is.]
Go on to Part 4, or read the Further Discussion below.
| 




![]()